Нихиль Будума - Основы глубокого обучения

Легко показать, что линейный персептрон и нейронная модель полностью эквивалентны. И просто продемонстрировать, что одиночные нейроны более выразительны, чем линейные персептроны. Каждый из них может быть выражен в виде одиночного нейрона, но последние могут также отражать модели, которые нельзя выразить с помощью линейного персептрона.

Одиночные нейроны мощнее линейных персептронов, но не способны решить сложные проблемы обучения. Поэтому наш мозг состоит из множества нейронов. Например, при помощи одного из них невозможно различить написанные от руки цифры. И чтобы решать более сложные задачи, нам нужны модели машинного обучения.

Нейроны в человеческом мозге расположены слоями. Его кора, по большей части отвечающая за интеллект, состоит из шести слоев. Информация перетекает по ним, пока сенсорные данные не преобразуются в концептуальное понимание [7]. Например, самый нижний слой визуальной зоны коры получает необработанные визуальные данные от глаз. Эта информация преобразуется в каждом следующем слое и передается далее, пока на шестом слое мы не заключаем, что видим кошку, банку газировки или самолет. На рис. 1.9 показан упрощенный вариант этих слоев.

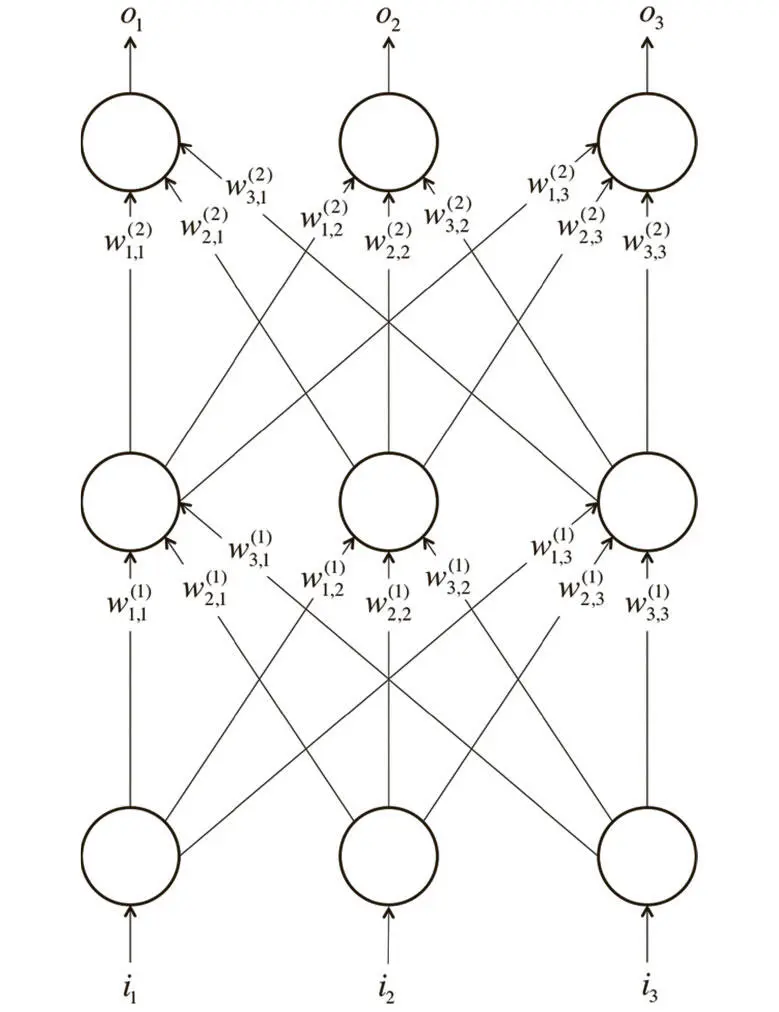
Рис. 1.9. Простой пример нейросети с прямым распространением сигнала с тремя слоями (входной, скрытый, выходной) и тремя нейронами на каждый слой

На основе этих идей мы можем создать искусственную нейросеть . Она возникает, когда мы начинаем соединять нейроны друг с другом, со входными данными и выходными узлами, которые соответствуют ответам сети на изучаемую задачу. На рис. 1.9 показан простейший пример искусственной нейросети, схожей по архитектуре с той, что была описана в 1943 году в работе Маккаллоу и Питтса. В нижний слой поступают входные данные. Верхний (выходные узлы) вычисляет ответ. Средний слой (слои) нейронов именуется скрытым, и здесь 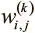— вес соединения i-го нейрона в k-м слое с j-м нейроном в ( k + 1) — м слое . Эти веса образуют вектор параметров θ, и, как и ранее, наша способность решать задачи при помощи нейросетей зависит от нахождения оптимальных значений для θ.

В этом примере соединения устанавливаются только от нижних слоев к верхним. Отсутствуют связи между нейронами одного уровня, нет таких, которые передают данные от высшего слоя к низшему. Подобные нейросети называются сетями с прямым распространением сигнала , и мы начнем с них, потому что их анализировать проще всего. Такой разбор (процесс выбора оптимальных значений для весов) мы предложим в главе 2. Более сложные варианты связей будут рассмотрены в дальнейших главах.

Ниже мы рассмотрим основные типы слоев, используемые в нейросетях с прямым распространением сигнала. Но для начала несколько важных замечаний.

1. Как мы уже говорили, слои нейронов между первым (входным) и последним (выходным) слоями называются скрытыми. Здесь в основном и происходят волшебные процессы, нейросеть пытается решить поставленные задачи. Раньше (как при распознавании рукописных цифр) мы тратили много времени на определение полезных свойств; эти скрытые слои автоматизируют процесс. Рассмотрение процессов в них может многое сказать о свойствах, которые сеть научилась автоматически извлекать из данных.

2. В этом примере у каждого слоя один набор нейронов, но это не необходимое и не рекомендуемое условие. Чаще в скрытых слоях нейронов меньше, чем во входном: так сеть обучается сжатому представлению информации. Например, когда глаза получают «сырые» пиксельные значения, мозг обрабатывает их в рамках границ и контуров. Скрытые слои биологических нейронов мозга заставляют нас искать более качественное представление всего, что мы воспринимаем.

3. Необязательно, чтобы выход каждого нейрона был связан с входами всех нейронов следующего уровня. Выбор связей здесь — искусство, которое приходит с опытом. Этот вопрос мы обсудим детально при изучении примеров нейросетей.

4. Входные и выходные данные — векторные представления. Например, можно изобразить нейросеть, в которой входные данные и конкретные пиксельные значения картинки в режиме RGB представлены в виде вектора (см. рис. 1.3). Последний слой может иметь два нейрона, которые соотносятся с ответом на задачу: [1, 0], если на картинке собака; [0, 1], если кошка; [1, 1], если есть оба животных; [0, 0], если нет ни одного из них.

Заметим, что, как и нейрон, можно математически выразить нейросеть как серию операций с векторами и матрицами. Пусть входные значение i-го слоя сети — вектор x = [ x 1 x 2… x n ]. Нам надо найти вектор y = [ y 1 y 2 … y m ], образованный распространением входных данных по нейронам. Мы можем выразить это как простое умножение матрицы, создав матрицу весов размера n × m и вектор смещения размера m . Каждый столбец будет соответствовать нейрону, причем j-й элемент сопоставлен весу соединения с j-м входящим элементом. Иными словами, y = ƒ ( W Tx + b), где функция активации применяется к вектору поэлементно. Эта новая формулировка очень пригодится, когда мы начнем реализовывать эти сети в программах.

Большинство типов нейронов определяются функцией активации f , примененной к логиту logit z . Сначала рассмотрим слои нейронов, которые используют линейную функцию f(z) = az + b . Например, нейрон, который пытается подсчитать стоимость блюда в кафе быстрого обслуживания, будет линейным, a = 1 и b = 0. Используя f(z) = z и веса, эквивалентные стоимости каждого блюда, программа присвоит линейному нейрону на рис. 1.10 определенную тройку из бургеров, картошки и газировки, и он выдаст цену их сочетания.

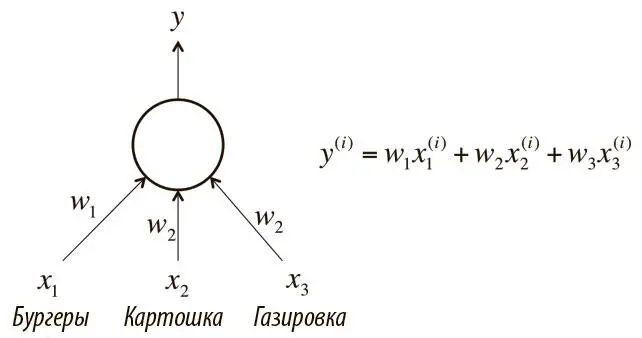
Рис. 1.10. Пример линейного нейрона

Вычисления с линейными нейронами просты, но имеют серьезные ограничения. Несложно доказать, что любая нейросеть с прямым распространением сигнала, состоящая только из таких нейронов, может быть представлена как сеть без скрытых слоев. Это проблема: как мы уже говорили, именно скрытые слои позволяют узнавать важные свойства входных данных. Чтобы научиться понимать сложные отношения, нужно использовать нейроны с определенного рода нелинейностью.