Нихиль Будума - Основы глубокого обучения

В глобально нормализованной сети интерпретация результатов будет немного другой. Вместо того чтобы прогонять их через функцию мягкого максимума для получения распределения вероятностей каждого действия, мы суммируем все результаты последовательности действий гипотезы. Один из способов выбрать верную последовательность — рассчитать такую сумму по всем гипотезам и наложить на результаты слой функции мягкого максимума, получив распределение вероятностей. Теоретически можно использовать ту же функцию потерь перекрестной энтропии, что и в локально нормализованной сети. Но эта стратегия сопряжена с проблемой: число возможных гипотез последовательности невероятно велико. Даже если взять предложение со средней длиной 10 и консервативной оценкой общего числа действий в 15, один сдвиг и по семь меток для левой и правой дуг, гипотез получится 1 000 000 000 000 000.

Чтобы разобраться с этой проблемой, мы, как показано на рис. 7.12, применяем лучевой поиск с фиксированным размером луча, пока либо не достигнем конца предложения, либо верная последовательность действий не появится на луче. После этого мы строим функцию потерь, которая будет поддерживать «золотой стандарт» последовательности действий (выделенный голубым цветом) как можно выше на луче, максимизируя его оценку по сравнению с другими гипотезами. Не будем вдаваться в подробности создания этой функции, детали описаны в работе Андора и коллег [88]. В ней также показан более изощренный разметчик частей речи, который использует глобальную нормализацию и лучевой поиск и тем самым значительно увеличивает точность по сравнению с разметчиком, который мы создали в этой главе.

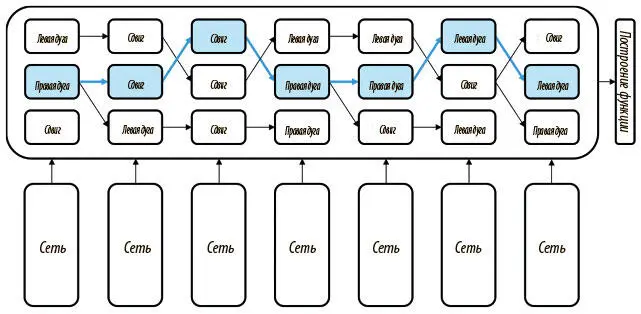
Рис. 7.12. Реализовать глобальную нормализацию в SyntaxNet можно, если сочетать обучение и лучевой поиск

Мы уже рассмотрели несколько хитростей, позволяющих приспособить сети c прямым распространением сигнала к анализу последовательностей, но нам еще предстоит найти изящное решение. В примере с разметкой частей речи мы прямо предположили, что можем игнорировать долгосрочные зависимости. Нам удалось преодолеть ряд ограничений, введя понятия лучевого поиска и глобальной нормализации, но все равно поле действия было ограничено ситуациями, в которых возможно однозначное соответствие между элементами входной и выходной последовательностей. Даже в модели разбора зависимостей пришлось переформулировать проблему, чтобы найти такое соответствие между рядом конфигураций входных данных при создании дерева разбора и действиями над стандартными дугами.

Иногда задача куда сложнее нахождения однозначных соответствий между входной и выходной последовательностями. Например, мы хотим построить модель, которая может сразу принимать все предложение и делать вывод, положительна или отрицательна его эмоциональная окраска. В этой главе мы построим простую модель, способную решать эту задачу. Или нам может понадобиться алгоритм, который будет получать комплексные входные данные (например, изображение) и порождать предложение (слово за словом), его описывающее. Можно даже попробовать перевести предложения с одного языка на другой (например, с английского на французский). Во всех этих случаях нет однозначной очевидной связи между символами на входе и выходе. Процесс больше напоминает ситуацию, приведенную на рис. 7.13.

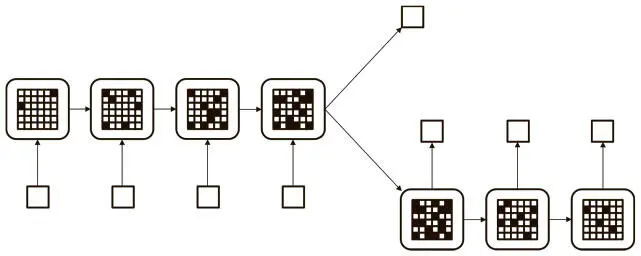
Рис. 7.13. Идеальная модель анализа последовательностей может хранить информацию в памяти долгое время, порождая устойчивый «мыслительный» вектор, который используется для нахождения ответа

Идея проста. Мы хотим, чтобы наша модель сохраняла какую-то память при считывании входной последовательности. В процессе чтения она должна быть способна изменять банк памяти, учитывая получаемую информацию. Когда она достигнет конца входной последовательности, внутренняя память должна содержать «мысль», представляющую ключевые элементы информации, то есть смысл входных данных. Затем мы, как показано на рис. 7.13, можем с помощью этого вектора мысли либо создать метку для исходной последовательности, либо породить соответствующую выходную последовательность (перевод, описание, резюме и т. д.).

В предыдущих главах эта идея не рассматривалась. Сети с прямым распространением сигнала по природе своей не имеют «состояний». После обучения любая из них становится статичной. Она не может ни переключать память между разными входными данными, ни изменять способы их обработки на основе входных данных, с которыми имела дело в прошлом. Чтобы реализовать эту стратегию, придется пересмотреть архитектуру нейронных сетей и начать создавать модели глубокого обучения с фиксацией состояния. Вернемся к рассмотрению сетей на уровне нейронов. В следующем разделе поговорим о том, как рекуррентные связи (в отличие от прямых, которые мы рассматривали ранее) позволяют моделям фиксировать состояние, и опишем класс моделей, известных как рекуррентные нейронные сети (РНС) .

Первые РНС были предложены в 1980-е годы, но популярность обрели лишь недавно благодаря нескольким интеллектуальным и техническим прорывам, которые помогли повысить их обучаемость. РНС отличаются от сетей с прямым распространением сигнала, потому что в них используется особый тип нейронного слоя, именуемый рекуррентным и позволяющий сети сохранять свое состояние в промежутках между сеансами ее использования.

На рис. 7.14 показана нейронная архитектура рекуррентного слоя. У всех нейронов есть входные соединения, приходящие от всех нейронов предыдущего слоя, и выходные, ведущие ко всем нейронам последующего. Однако эти типы соединений для рекуррентного слоя не единственные. В отличие от слоя с прямым распространением сигнала, он обладает рекуррентными соединениями, которые распространяют информацию между нейронами одного слоя. В полносвязном подобном слое информационный поток идет от каждого нейрона к каждому нейрону того же слоя (в том числе и к себе). У такого слоя с числом нейронов r есть r 2 рекуррентных соединений.

Рис. 7.14. Рекуррентный слой содержит рекуррентные соединения между нейронами, расположенными на одном уровне

Чтобы лучше понять, как работает РНС, рассмотрим ее функционирование после соответствующего обучения. Каждый раз, когда нам нужно обработать очередную последовательность, мы создаем новый экземпляр нашей модели.