Нихиль Будума - Основы глубокого обучения

Можно работать с сетями, содержащими рекуррентные слои, разделив срок жизни экземпляра сети на дискретные временные шаги. На каждом шаге мы вводим в модель следующий элемент данных. Прямые соединения отражают информационный поток от одного нейрона к другому, в котором передаваемые данные — подсчитанная нейронная активация на текущем шаге. В случае же рекуррентных связей данные — сохраненная нейронная активация на предыдущем шаге. Таким образом, активации нейронов здесь отражают накапливаемое состояние экземпляра сети. Изначальные активации нейронов в рекуррентном слое — параметры нашей модели, и их оптимальные значения мы определяем точно так же, как лучшие значения для весов каждого соединения в процессе обучения. Оказывается, при фиксированном времени жизни (например, t шагов) экземпляра РНС мы можем выразить его в виде сети с прямым распространением сигнала, хоть и с нерегулярной структурой.

Это хитрое преобразование, показанное на рис. 7.15, часто именуется «разворачиванием» РНС во времени. Рассмотрим экземпляр РНС на рисунке. Нам нужно связать последовательность двух входов (каждый — размера 1) с одним выходом (тоже размера 1). Это преобразование мы осуществляем, взяв нейроны одного рекуррентного слоя и скопировав их t раз — по разу для каждого шага. Точно так же мы воспроизводим нейроны входного и выходного слоев. С каждым шагом мы копируем и прямые связи — такими, какими они были в исходной сети. Затем мы воссоздаем рекуррентные связи в виде прямых от каждой временной копии к следующей (поскольку такие связи отражают нейронную активацию предыдущего временного шага).

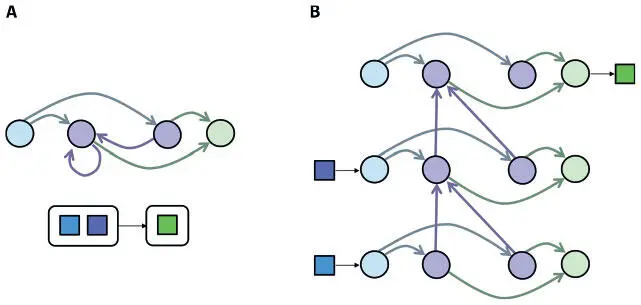
Рис. 7.15. Мы можем развернуть РНС во времени, чтобы выразить ее в виде сети с прямым распространением сигнала, которую можно обучить с помощью алгоритма обратного распространения ошибок

Теперь мы можем обучить РНС, вычислив градиент для развернутой версии. Это значит, что все алгоритмы обратного распространения ошибок, которые использовались для сетей с прямым распространением сигнала, подойдут и для РНС. Но есть одна проблема. После каждого пакета обучающих примеров необходимо изменить веса на основании вычисленных производных ошибок. В развернутой сети у нас есть наборы связей, и все они соответствуют одной связи из исходной РНС. А вот производные ошибок для этих развернутых связей не обязательно будут равны (на практике они чаще всего и не равны). Можно обойти эту проблему, усреднив или суммировав производные ошибок для всех связей одного набора. Это позволит использовать производную ошибок, учитывающую всю действующую на веса соединения динамику, при попытке заставить сеть выдать точный результат.

Мотивы использования модели сети с фиксацией состояния связаны с идеей отражения долгосрочных зависимостей во входной последовательности. Вроде бы логично предположить, что РНС с большим банком памяти (рекуррентным слоем значительного размера) сможет запомнить все эти зависимости. И действительно, теоретически еще в 1996 году Джо Килиан и Хава Сигельманн показали, что РНС — универсальное функциональное представление [89]. Иными словами, при достаточном количестве нейронов и правильной настройке параметров РНС можно использовать для представления любых функциональных зависимостей между входными и выходными последовательностями. Эта теория много обещает, но на практике реализуется не всегда. Хоть и полезно знать, что РНС может выразить любую произвольную функцию, лучше понимать, насколько практически полезно с нуля обучать ее реалистическим функциональным связям путем применения алгоритмов градиентного спуска. Если это непрактично, мы окажемся в затруднительном положении, так что рассмотреть вопрос нужно максимально строго. Начнем с анализа самой простой РНС из возможных (рис. 7.16): один входной нейрон, один выходной, полносвязный рекуррентный слой тоже с одним нейроном.

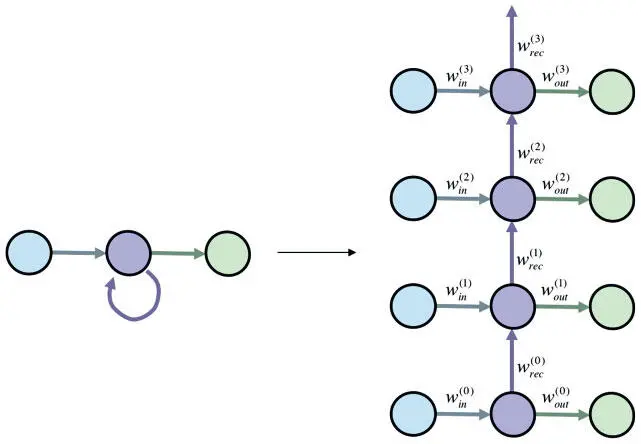
Рис. 7.16. Один нейрон в полносвязном рекуррентном слое (в сжатом и развернутом во времени видах) — пример анализа обучающих алгоритмов на основе градиента

Начнем с простого. При нелинейности f мы можем выразить активацию h (t) скрытого нейрона рекуррентного слоя на шаге t следующим образом, где i (t) — входной логит входного нейрона на временном шаге t :

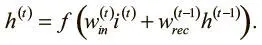
Попытаемся вычислить, как активация скрытого нейрона будет меняться в ответ на корректировки входящего логита в течение k шагов в прошлом. Анализ этого компонента градиентных выражений обратного распространения ошибок начнем с оценки того, сколько «памяти» сохраняется от предшествующих входных данных.

Сначала возьмем частную производную и применим правило дифференцирования сложной функции:

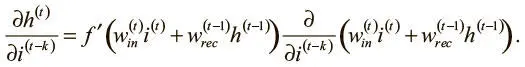
Поскольку значения весов входного и рекуррентного соединений не зависят от входного логита на временном шаге ( t − k), можно упростить выражение:

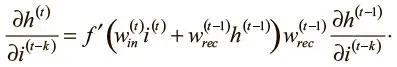
Поскольку нам интересна величина этой производной, можно взять абсолютное значение обеих сторон. Мы также знаем, что для всех обычных нелинейностей (гиперболического тангенса — tanh, логистической и ReLU) максимальное значение f ′ равно 1. Отсюда выводим следующее рекурсивное неравенство:

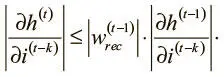
Можно продолжить рекурсивно расширять его, пока не дойдем до основного случая на шаге ( t − k):

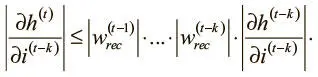
Оценить эту частную производную можно уже рассмотренным путем:

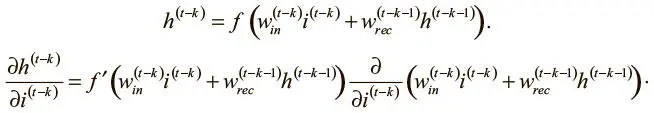
В этом выражении активация скрытого слоя на шаге ( t − k − 1) не зависит от значения входных данных на шаге ( t − k).

Поэтому мы можем переписать его:

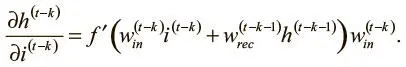
Наконец, взяв абсолютное значение для обеих сторон и вновь применив наблюдение относительно максимального значения f ′, можно записать: