Клаудио Фернандес-Араос - Выбор сильнейших. Как лидеру принимать главные решения о людях

Поисковая команда компании использовала простой, но эффективный метод сопоставления, заключавшийся во взвешивании пяти компетенций, признанных необходимыми, с последующей оценкой уровня каждой компетенции у каждого кандидата по шкале от 1 до 10. (Так как данная фирма по подбору часто занималась глобальной «калибровкой» кандидатов в мировом масштабе, вероятность «разнобоя» между разными странами была сведена к минимуму.) Затем вычислялся общий взвешенный показатель и дополнялся качественным описанием ключевых сильных и слабых сторон каждого кандидата, как внутреннего, так и внешнего.

Качественное сопоставление кандидатов предполагает, во-первых, определение четкого профиля лучшего на рынке внешнего кандидата и, во-вторых, – глубокое и объективное рассмотрение внутренних кандидатов. Давайте ознакомимся с примером международной программистской компании, основатели которой еще не отошли от управления. Компания вела поиск CEO и в конце концов остановила свой выбор на старшем руководителе из крупной технологической фирмы, который, в свою очередь, быстро нанял нескольких других руководителей из круга бывших коллег. Однако новая команда не смогла адаптироваться к существующей культуре и в конце концов была уволена в полном составе.

Последующий поиск выявил одного из внутренних старших руководителей, которого раньше просто «проглядели». Сравнительная оценка этого человека с двумя лучшими внешними претендентами ясно показала, что он был самым сильным кандидатом для позиции CEO – отчасти потому, что сохранение культуры (и стабильности) компании являлось главным приоритетом.

Давайте еще раз вернемся к моему первому проекту в Буэнос-Айресе, в ходе которого мне поручили найти менеджера по маркетингу и продажам для Quilmes – ведущего пивного бренда компании Quinsa.

Сколько кандидатов я должен был сгенерировать, чтобы быть уверенным в том, что смогу представить клиенту всех лучших кандидатов на эту позицию? Я решил найти и оценить не меньше сотни кандидатов, и это вошло у меня в привычку. Только не спрашивайте, откуда взялось это число! Наверное, я решил, что 10 будет слишком мало, а 1000 – невозможно много.

Эксперты по принятию решений всегда советуют не загонять себя в угол, ограничивая свой выбор {155}. Ученые, изучавшие случаи отбора кандидатов в CEO, пришли к выводу, что советы директоров должны задавать как можно более широкие рамки целевого пула кандидатов {156}. Чем больше, тем лучше. Но все-таки: как узнать, что пора остановиться?

Один из ответов на этот вопрос дали статистики, работавшие над «задачей о приданом», в которой султан желал проверить мудрость своего главного визиря, искавшего себе жену. Султан приказал собрать 100 девушек своего королевства и провести их перед визирем одну за другой. Визирю предстояло выбрать девушку с самым большим приданым. Конечно, он мог задать вопрос об этом каждой из них напрямую. Стоя перед потенциальной избранницей, он мог сделать выбор: взять ее в жены или позвать следующую. Но ему было запрещено возвращаться к тем девушкам, которые уже прошли перед ним ранее . Если он сумеет выбрать девушку с самым большим приданым, то возьмет ее в жены и останется на своей должности. Если не сумеет – его казнят.

Статистики показали, что в такой ситуации лучшей стратегией является «правило 37 процентов». Визирю следует спросить первых 37 девушек и запомнить наибольшую цифру приданого, которую назовет одна из них (обозначим эту цифру как Н). После этого, начиная с тридцать восьмой по счету девушки, он должен остановиться на первой, назвавшей цифру больше, чем Н. Так визирь обеспечит себе наивысшую вероятность правильности выбора и возможность сохранить голову на плечах.

Но «правило 37 процентов» имеет и очевидные ограничения. Во-первых, чтобы сделать окончательный выбор, вам надо провести как минимум 38 интервью (т. е. 37 + 1) из ста возможных, на самом же деле – наверняка больше. А если ваша база насчитывает 1000 кандидатов? У вас найдется время, чтобы оценить (как минимум!) 371 из них?

Некоторые исследователи рассматривали эту проблему под рубрикой «быстрое и экономичное принятие решений», пытаясь найти способы достижения лучших результатов на гораздо меньшей выборке кандидатов. Одна из групп, исповедующая принцип «меньше – это больше», обнаружила, что более простые правила, например «проверь дюжину» (то есть проанализируй 12 кандидатов и после этого начинай сравнивать следующих с лучшими из предыдущих), не только намного более экономичны (с точки зрения количества проанализированных кандидатов), но и более действенны {157}. Конечно, это правило не максимизирует вероятность выявления лучшего кандидата, но оно позволяет найти кандидата с наивысшей ожидаемой ценностью и при этом снижает вероятность откровенно неудачного выбора. Интересно, что правило «проверь дюжину» работает не только на выборках в количестве 100 кандидатов, но и на пулах в несколько тысяч человек.

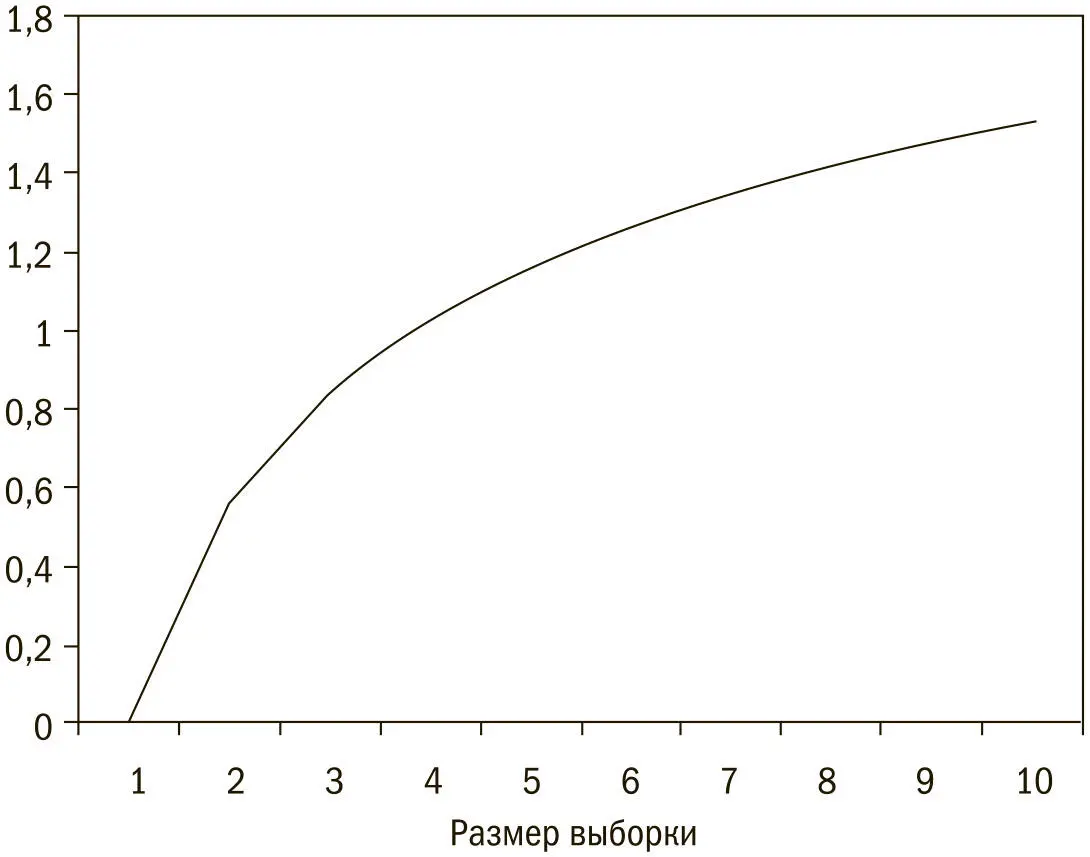
В этих изысканиях нет ничего удивительного, если принять в расчет статистику экстремальных величин. Если вы возьмете случайную выборку из нормального распределения, ожидаемая величина максимума будет расти с ростом размера выборки. Однако когда выборка будет достаточно большой, ожидаемая величина максимума уже не будет заметно расти с ростом размера выборки. Если вы рассмотрите стандартное нормальное распределение (у которого среднее значение равно 0 и стандартное отклонение равно 1) и возьмете выборку размером 1, то ожидаемое значение по определению будет равно 0. По мере роста размера выборки можно посчитать и ожидаемую величину максимума в этой выборке. Если мы возьмем очень большую выборку, то ее максимум, скорее всего, окажется в районе 2 (число 2 по определению равняется двум стандартным отклонениям от среднего, что в нормальном распределении должно случаться с небольшой вероятностью).

На рис. 6.3 показана ожидаемая величина максимума такого распределения в зависимости от размера выборки. Как видно, выборка размером 10 экземпляров дает ожидаемую величину, близкую к 1,6, что не так уж далеко от практического максимума (т. е. 2). Это объясняет действенность стратегии «проверь дюжину» в ситуации выбора кандидатов из очень большого пула.

Рис. 6.3.Ожидаемая величина максимума стандартного нормального распределения

Не стоит думать, однако, что, рассмотрев 12 кандидатов, вы можете успокоиться. К сожалению, все не так просто, поскольку мы имеем дело с взаимным выбором. Иными словами, человек, которого вы выбираете, должен также выбрать вас .