Владимир Брюков - Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews

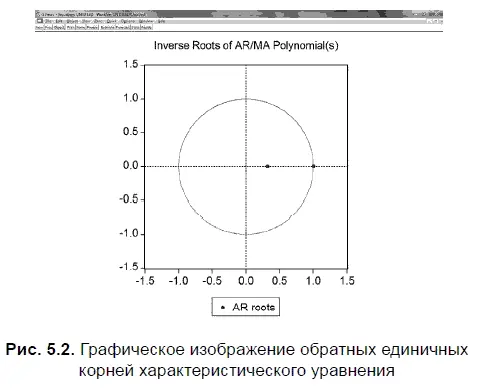
Теперь остановимся несколько подробнее на процедуре получения обратных единичных корней, с помощью которой в EViews доказывается стационарность AR-процессов. В главе 4 уже говорилось, что в основе теории единичного корня лежит довольно простая формула (4.4), которая считается базовой для понимания стационарности в уравнениях авторегрессии:

При этом уравнение авторегрессии 1-го порядка считается стационарным в том случае, когда коэффициент регрессии ρ < 1. Соответственно, если ρ > 1, то оно считается нестационарным, а следовательно, волатильность в процессе авторегрессии с течением времени может нарастать и стремиться к бесконечности.

Применительно к авторегрессионным процессам, содержащим большое количество лаговых переменных, наличие стационарности предполагает следующее. AR-процессы считаются стационарными в том случае, если в уравнении (5.2) коэффициенты а 1, а 2…., а р образуют сходящийся ряд и все корни характеристического уравнения 1 — a 1 Z — a 2 Z 2— … — a pZ p = 0 (вещественные и комплексные) должны лежать вне единичного круга (см. рис. 5.2), их абсолютное значение (по модулю) должно быть больше единицы.

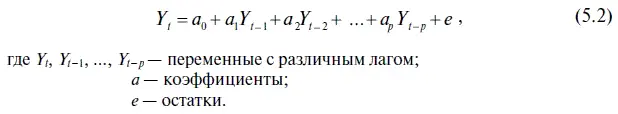
Например, для решенного нами уравнения авторегрессии USDOLLAR = 1,321092 × USDOLLAR(-l) — 0,319415 × USDOLLAR(-2) (см. формулу (4.3)) характеристическое уравнение приобретает следующий вид:

1 — 1,321092 Y t -1+ 0,319415 Y 2 t -1= 0. (5.3)

Корни в этом уравнении находятся с помощью известной со школьной скамьи формулы по нахождению корней в многочлене второй степени:

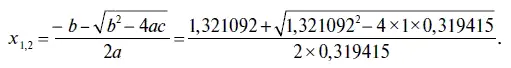
Отсюда следует, что первый единичный корень x 1= 3,138429, а второй х 2= 0,997545. Таким образом, один из этих двух корней характеристического уравнения лежит внутри единичного круга, а потому этот авторегрессионный процесс нельзя назвать стационарным. Однако мы уже говорили, что в EViews находятся не просто единичные корни, а именно ОБРАТНЫЕ единичные корни, которые мы получаем в выводе итогов (см. табл. 5.1) после небольших дополнительных вычислений. При этом первый и второй обратные единичные корни находятся из обычных единичных корней, полученных из уравнения (5.3), следующим образом: х 1 = 1: 3,138429 = 0,318631, а второй х 2 = = 1: 0,997545 = 1,002461.

По сути, тот факт, что вместо единичных корней мы находим обратные единичные корни, ничего не меняет, однако — и это вполне понятно — при этом требования к тестированию стационарности AR-процесса формулируются противоположным образом. В этом случае авторегрессионный процесс считается стационарным тогда и только тогда, когда абсолютные значения (по модулю) всех обратных корней его характеристического уравнения лежат в пределах единичного круга. Поскольку один из обратных корней больше единицы, то, следовательно, AR-процесс, описанный формулой 1,321092 × USDOLLAR(-l) — 0,319415 × USDOLLAR(-2), нельзя считать стационарным.

Теперь остановимся еще на одном важном инструменте, который дает EViews для оценки устойчивости статистических моделей к внешним шокам (в нашем случае под ними подразумеваются резкие скачки курса доллара). Это тестирование AR-структуры авторегрессионного процесса на импульсный ответ (IMPULSE RESPONSE). При этом у нас появляется возможность получить также и оценку инновационной неопределенности, возникающей в этом авторегрессионном процессе в результате воздействия внешнего шока.

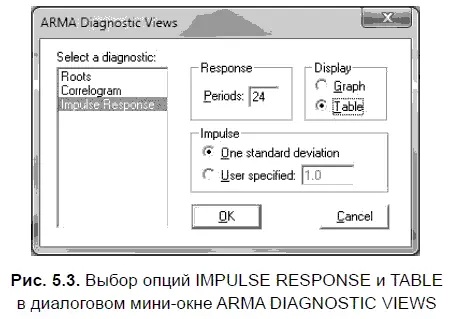
Чтобы провести исследование AR-структуры на импульсный ответ (IMPULSE RESPONSE), нам необходимо в диалоговом мини-окне ARMA DIAGNOSTIC VIEWS (посмотреть диагностику ARMA) выбрать опции IMPULSE RESPONSE и TABLE, а также определить предполагаемую величину импульса (внешнего шока или величину отклонения курса доллара) (рис. 5.3). При этом по умолчанию используется опция ONE STANDARD DEVIATION (одно стандартное отклонение), а длительность проводимого теста ограничивается 24 периодами (см. опцию PERIODS). Однако при необходимости количество тестируемых периодов можно изменить, как, впрочем, изменить и заданную величину импульса. В последнем случае надо в опции IMPULSE выбрать вариант USER SPECIFIED (по усмотрению пользователя) и самому установить требуемую величину начального импульса (внешнего шока).

В опции IMPULSE мы решили выбрать вариант по умолчанию — ONE STANDARD DEVIATION (одно стандартное отклонение). В случае выбора этой опции исходная величина внешнего шока приравнивается к стандартной ошибке коэффициента регрессии факторной лаговой переменной, т. е. к стандартной ошибке коэффициента регрессии USDOLLAR(-1) = 0,06527. При этом предполагается, что на первом шаге, когда внешний шок отсутствует, величина импульсного ответа равна стандартной ошибке уравнения регрессии -0,817803 (см. табл. 4.1).

В результате получим табл. 5.3, в которой содержится информация, характеризующая величину стандартной ошибки импульсного ответа AR-структуры на рост инновационной неопределенности, значения которой помещены в двух разделах Std. Err. Если бы вместо опции ONE STANDARD DEVIATION была бы выбрана опция USER SPECIFIED (по усмотрению пользователя), то тогда вместо величины инновационной неопределенности мы получили бы в разделах Std. Err. величину внешнего шока в виде стандартных ошибок факторной переменной, нарастающей по мере повышения инновационной неопределенности.

Таким образом, величина стандартной ошибки функции импульсного ответа позволяет оценить, как модель ARMA реагирует на единовременное шоковое воздействие (однократное резкое изменение курса доллара). В таблице 5.3 также приводится величина стандартной ошибки функции накопленного импульсного ответа. Последнюю функцию можно интерпретировать и как ответ на очередной текущий импульс (шоковое воздействие), но при условии, что аналогичные шоковые воздействия происходят непрерывно в течение всего исследуемого времени, начиная с 1-го периода.