Владимир Брюков - Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews

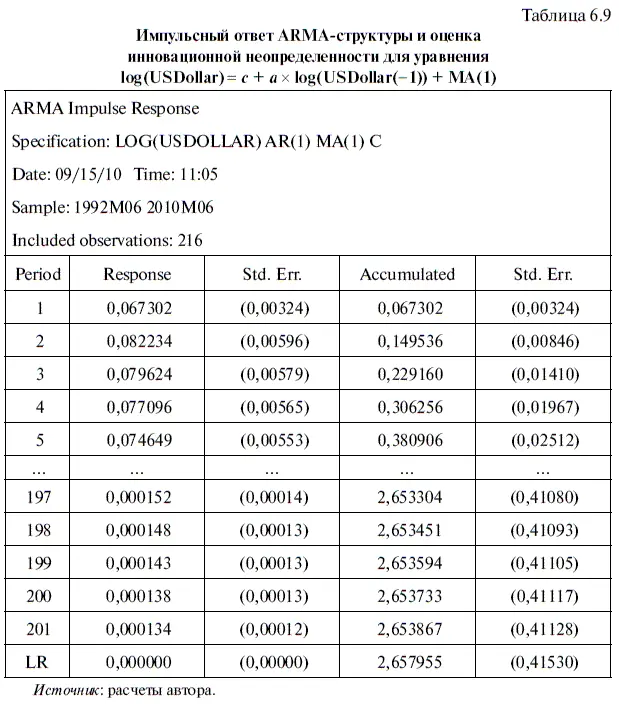
Кроме того, в табл. 6.9 хорошо видно, что по мере увеличения количества исследуемых периодов величина стандартного отклонения у накопленного импульсного ответа (см. раздел таблицы Accumulated) и уровень накопленной инновационной неопределенности (см. раздел в центре таблицы — Sid. Err.) стремятся к определенному асимптотическому пределу, значение которого приводится внизу. Следует заметить, что у статистической модели с нестационарной ARMA-структурой указанный предел отсутствует.

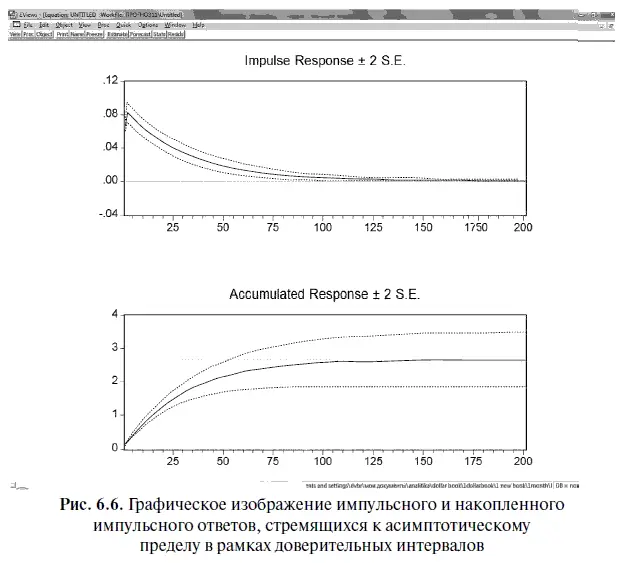
В целях экономии места в табл. 6.9 приведена лишь часть данных. Однако эта информация в наглядном виде представлена на рис. 6.6, который полностью подтверждает наши выводы. Кроме того, на рисунке точечными линиями с двух сторон обозначены доверительные интервалы, показывающие возможную погрешность в оценке величины импульсного и накопленного импульсного ответов.

Насколько хорошо построена стационарная модель, можно судить по оценке соответствия фактических значений коррелограммы остатков их теоретическим значениям. С этой целью воспользуемся опциями VIEW/ARMA STRUCTURE (посмотреть/структура модели ARMA). В результате на экране появится диалоговое мини-окно ARMA DIAGNOSTIC VIEWS (посмотреть диагностику модели ARMA), в которой нужно выбрать параметр CORRELOGRAM (рис. 6.7). Причем если нам нужна коррелограмма в табличной форме, то в опции DISPLAY мы выбираем надпись TABLE, а если в виде графика, то следует выбрать надпись GRAPH. При этом по умолчанию составляется коррелограмма для 24 лагов, но при необходимости пользователь может выбрать и иное количество лагов.

В таблице 6.10 представлены как фактические, так и теоретические значения коррелограммы остатков, полученных после решения уравнения регрессии log(USDollar) = с + а × log(USDollar(—1)) + МА(1). В таблице представлены значения автокорреляционной и частной автокорреляционной функций (т. е. автокорреляция между двумя лагами без учета влияния других промежуточных временных лагов). Как вычисляются коэффициенты автокорреляции и частной автокорреляции, можно уточнить в формулах (3.7–3.9).

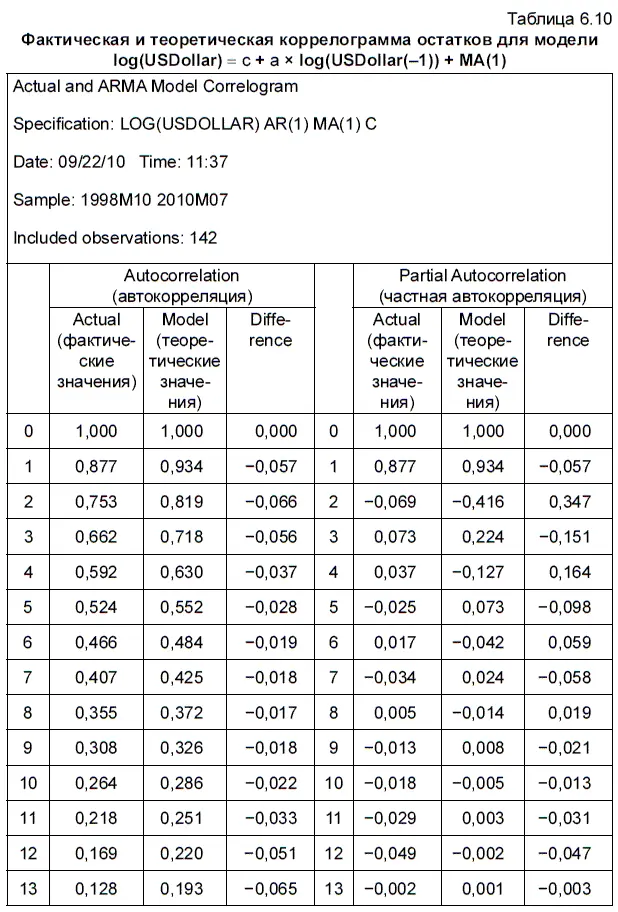
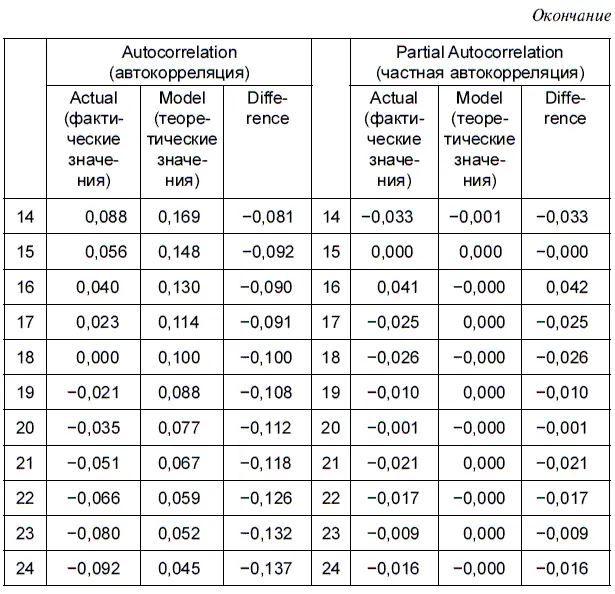
Важной особенностью коррелограммы остатков, полученных по стационарным моделям, является то, что с увеличением величины лага значения автокорреляционной функции медленно, но с завидным постоянством убывают к нулю, в то время как частная автокорреляционная функция начинает колебаться около нуля уже со второго лага, при этом то немного вырастая, то убывая.

Стационарная модель считается хорошо построенной, если фактические значения коррелограммы окажутся близкими к ее теоретическим значениям. Как видим, в этом случае у нас это получилось.

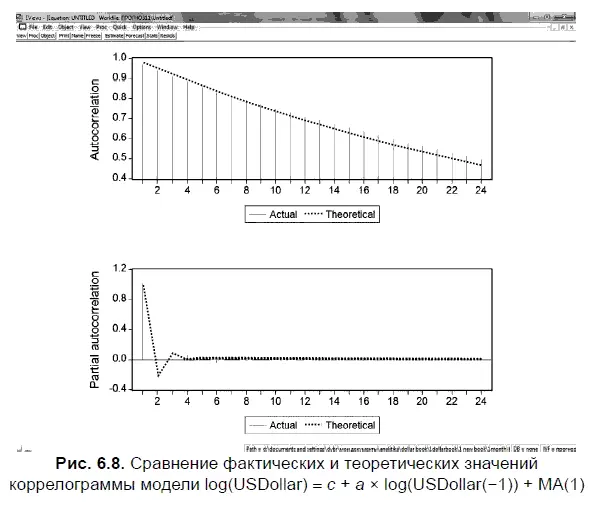
Близость между фактическими и теоретическими значениями коррелограммы наглядно представлена на рис. 6.8. При этом теоретические значения коррелограммы с целью большей наглядности обозначены на рисунке горизонтальной линией, а фактические значения вертикальными линиями.

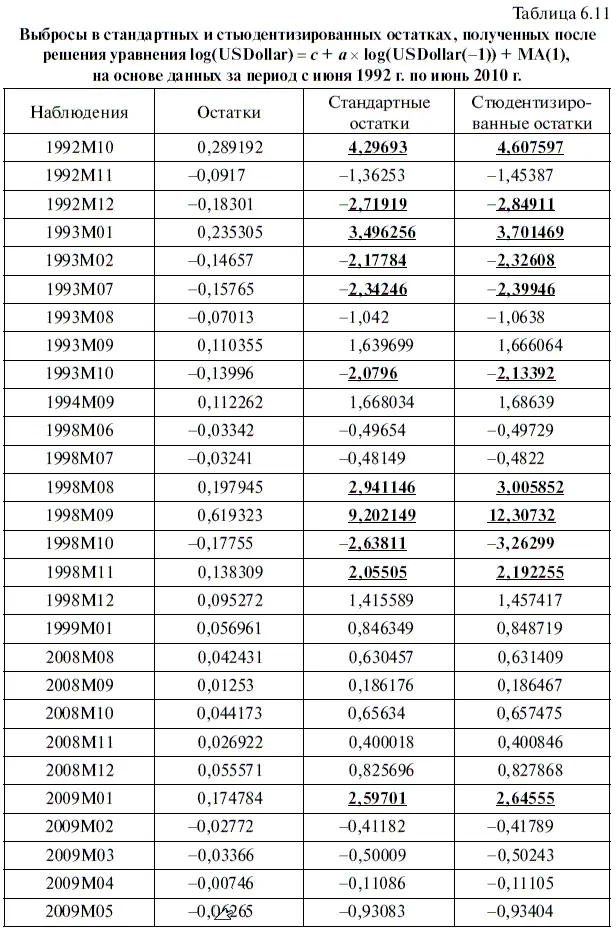
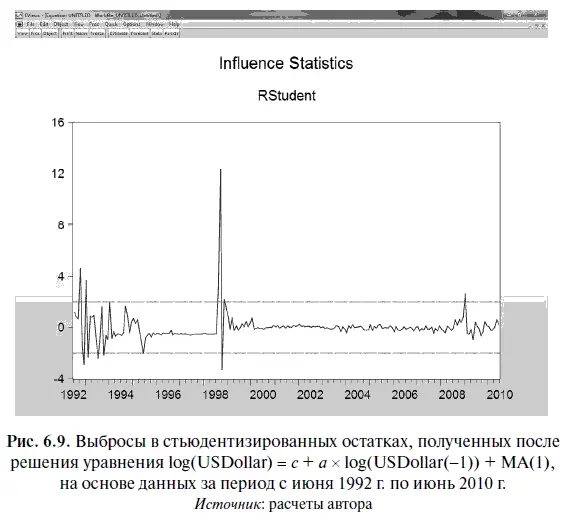
На основе данных за период с июня 1992 г. по июнь 2010 г. необходимо с помощью модели log(USDollar) = с + а × log(USDollar(-1)) + МА(1) составить точечный и интервальный прогнозы по курсу доллара на июль 2010 г. Однако прежде проведем анализ стандартных и стьюдентизированных остатков, полученных в этой модели, на предмет наличия выбросов, причем особое внимание будем обращать на наличие выбросов в последних наблюдениях, которые в большей степени могут повлиять на точность текущего прогнозирования. Для расчета стандартных и стьюдентизированных остатков следует воспользоваться алгоритмами действий № 16 и 17.

В результате у нас получилась табл. 6.11, а также диаграмма стьюдентизированных остатков на рис. 6.9. Если эту таблицу сравнить с табл. 5.9, то выяснится следующее важное обстоятельство. В статистической модели log(USDollar) = с + а × log(USDollar(-l)) + МА(1)из 11 выбросов, выявленных с помощью стандартных и стьюдентизированных остатков, шесть выбросов приходятся на период 1992–1993 гг., т. е. имели место в период самых первых наблюдений. В свою очередь остальные четыре выброса произошли с августа по ноябрь 1998 г., в период после дефолта. В то же время в период глобального финансового кризиса в остатках этой модели обнаруживается лишь один выброс, относящийся к январю 2009 г.

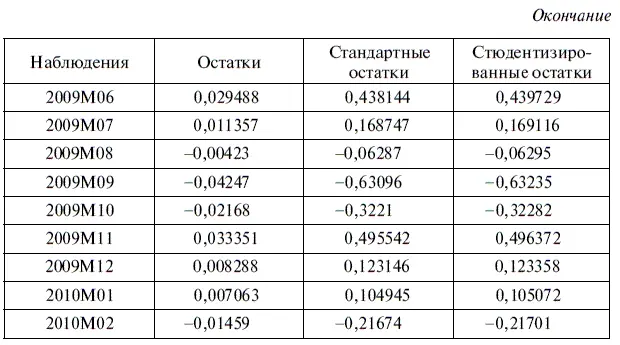
Для справки заметим, что в остатках, получившихся после решения уравнения регрессии USDOLLAR = а × USDOLLAR(-l) + b × USDOLLAR(-2), имели место девять выбросов. Причем до августа 1998 г. в этой модели выбросы не выявлены, но зато было пять выбросов после августовского дефолта — с августа по декабрь 1998 г. и четыре выброса в период глобального финансового кризиса — в январе, феврале, марте и мае 2009 г. Таким образом, в последние годы стационарная модель log(USDollar) = с + а × log(USDollar(-l)) + МА(1) демонстрирует гораздо большую стабильность, чем нестационарная модель USDOLLAR = а × USDOLLAR(-l) + b × USDOLLAR(-2).

На рисунке 6.9 приведена диаграмма, из которой хорошо видно, что, за исключением одного уже упомянутого случая, выбросы в стационарной модели после 1998 г. уже не наблюдались.

В главе 4 уже говорилось, что тест Чоу на точность прогноза хорошо подходит для анализа стабильности статистической модели относительно последнего наблюдения. Поэтому мы воспользовались этим тестом, чтобы еще раз убедиться в стабильности модели log(USDollar) = с + а × log(USDollar(-l)) + МА(1) относительно июня 2010 г. (см. алгоритм действий № 19). В результате у нас получилась табл. 6.12. Судя по уровню значимости F -критерия ( F-statistic ) и логарифма правдоподобия (Log likelihood ratio), можно сделать вывод, что нулевая гипотеза о структурной стабильности статистической модели относительно последнего наблюдения подтверждается с большим уровнем надежности. Отметим еще раз, что нулевая гипотеза может быть отвергнута, если уровень значимости (Probability) F -критерия и логарифма правдоподобия будет ниже 0,05.