Александр Волошинов - Математика и искусство

Важнейшим преимуществом количественного языка математики является краткость и точность. В этом его огромное преимущество и в этом его красота, ибо именно в математическом языке претворяется один из основных признаков красоты в науке: сведение сложности к простоте. Всем известно, что с помощью математического языка — функций, уравнений, формул — точно и кратко описываются самые разнообразные свойства и явления, происходящие в природе и обществе. Древнегреческому математику Апполонию из Перги (ок. 260 — ок. 170 гг. до н. э.) потребовалось восемь книг, чтобы описать свойства конических сечений. Между тем на языке аналитической геометрии, т. е. с помощью алгебраических формул, эти свойства доказываются на нескольких страницах. Эталоном простоты и красоты, символом современной физики стала знаменитая формула Эйнштейна

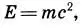
выражающая в простой и изящной математической форме глубокие физические идеи.

Математика: прекрасное в науке

Итак, математика — это не только самостоятельная наука о "математических структурах", но и язык других наук, язык единый, универсальный, точный, простой и, следовательно, "красивый. Хорошо сказал об этих качествах математики наш современник, замечательный советский математик С. Л. Соболев, в 31 год ставший академиком: "Есть одна наука, без которой невозможна никакая другая. Это математика. Ее понятия, представления и символы служат языком, на котором говорят, пишут и думают другие науки. Она объясняет закономерности сложных явлений, сводя их к простым, элементарным явлениям природы. Она предсказывает и предвычисляет далеко вперед с огромной точностью ход вещей".

Последнее свойство математики, о котором говорит Соболев, дающее возможность "выспрашивать" у природы ее тайны и позволяющее делать потрясающие воображение открытия "на кончике пера", ставит математику в исключительное положение среди наук. Классическим примером триумфа математики в естествознании стало открытие планеты Нептун. Его история такова. Еще в XVIII веке (вскоре после открытия планеты Уран) в ее движении астрономы обнаружили некоторые "неправильности". Тогда же было высказано предположение о том, что эти отклонения орбиты вызваны притяжением неизвестной еще планеты. Однако только к середине XIX века параметры орбиты Неизвестной планеты были вычислены независимо друг от Друга англичанином Джоном Адамсом (1819-1892) и Французом Урбеном Леверье (1811 — 1877). Результаты вычислений Адаме в сентябре 1845 г. передал в Гриничскую обсерваторию (Великобритания), а Леверье 18 сентября 1846 г. послал в Берлинскую обсерваторию.

Но если расчеты Адамса продолжали пылиться в архивах Гринвичской обсерватории, то по расчетам Леверье 23 сентября 1846 г., в первый же вечер после получения письма от Леверье, немецкий астроном Иоганн Галле (1812-1910) обнаружил неизвестную планету точно в указанном месте небосвода! Как видим, история научных открытий полна драматизма. Открытие Нептуна было величайшим триумфом математики: далекая неизвестная планета была найдена в кабинете ученого только с помощью карандаша и бумаги, т. е. с помощью математики!

Наука чистой математики в ее современных вариантах может быть представлена в качестве самого оригинального продукта человеческого духа. Другим претендентом на это звание является музыка.

Математика: прекрасное в науке

Последующие сто лет истории науки были цепью блестящих побед и предсказаний математики и в других науках. И ядерная физика, и освоение космоса немыслимы без математики! Одним из последних открытий "на кончике пера" является открытие физического эффекта Т-слоя в плазме, сделанное группой советских ученых под руководством академиков А. Н. Тихонова и А. А. Самарского. Правда, вместо карандаша и бумаги современные математики располагают мощными ЭВМ, но суть остается той же: математические уравнения предсказывают физические явления.

В этом удивительном свойстве математики, называемом эвристическим (от архимедовой "эврики"), заключено высшее выражение еще одного признака красоты в науке — обретение неочевидной истины. Роль математики в постижении неочевидных истин, а значит, и красота математики непревзойдены.

"Непостижимая эффективность математики в естественных науках" — так называется знаменитая статья Вигнера и так с его легкой руки называют теперь это свойство математики. "Чудесная загадка соответствия математического языка законам физики является удивительным даром, который мы не в состоянии понять и которого мы, возможно, недостойны. Мы должны испытывать чувство благодарности за этот дар. Следует надеяться, что он не покинет нас в будущих исследованиях и что он будет — хорошо это или плохо — развиваться к нашему большому удовлетворению, а быть может, и к нарастающему беспокойству, расширяя область познания окружающего нас мира". Эти слова Ю. Вигнера — взволнованный гимн математике. Правда, в них звучит и растерянность перед необъяснимой загадкой, которая, как и в случае с Н. Бурбаки, вызвана философскими заблуждениями автора.

Математика: прекрасное в науке

Большинство математиков склонны видеть "непостижимую эффективность" воей науки в глубинных связях с реальным миром. Так считает и выдающийся мериканский математик, один из создатели ЭВМ, Дж. фон Нейман (1903-1957). развитые математические идеи, отмечает Нейман, начинают жить собственной лсизнью, благодаря чему математика становится похожей на искусство. Но слова Неймана служат и предостережением некоторым "эстетам от математики", ибо отрыв от реальности делает "математику для математики", как и "искусство для искусства", чахлым декадентским течением.

Но в одном вопросе сходятся все ученые: математика является символом мудрости науки, образцом научной строгости и простоты, эталоном совершенства и красоты в науке. Вот только несколько высказываний по этому поводу.

"Математические доказательства, как алмазы, тверды и прозрачны и поддаются лишь самой строгой логике".

"Творчество математика в такой же степени есть создание прекрасного, как творчество живописца или поэта,- совокупность идей, подобно совокупности красок или слов, должна обладать внутренней гармонией. Красота есть первый пробный камень для математической идеи; в мире нет места уродливой математике".