Александр Волошинов - Математика и искусство

Вселенная своей неизмеримой громадностью, безграничным разнообразием и красотой, которые сияют в ней со всех сторон, повергает дух в немое удивление.

Две вещи наполняют душу всегда новым и все более сильным удивлением и благоговением...- это звездное небо надо мной и моральный закон во мне.

Математика: прекрасное в науке

Математика: прекрасное в науке

Итак, стремясь дать новое определение прекрасного, Волькенштейн пытается найти признаки красоты в науке: математике, физике, химии. Эти признаки, по Волькенштейну, таковы: 1) эстетическое впечатление "возникает только в связи с целесообразным, сложным (трудным) преодолением"; 2) "красиво сведение сложности к простоте"; 3) "всякое математическое оформление научных достижений, если оно наглядно и гармонично, вызывает эстетическое впечатление".

Легко видеть, что формула "красота есть целесообразное, трудное преодоление" перекликается с формулой Хатчесона "красота есть обретение неочевидной истины". Да, Природа прячет свои законы в сокровенных тайниках и открываются они только тому, у когс хватает сил на трудное преодоление. И как вознаграждение в конце пути ожидает ученого красота открывающейся истины. Альберт Эйнштейн (1879-1955) любил повторять, что Бог (т. е. Природа) изощрен но не злонамерен (эта надпись была сделана у Эйнштейна на камине). Изощренность Природы состоит в том что она ловко скрывает от человека свои законы, а ю внешнее проявление выглядит поначалу как полный хаос. Не злонамеренность же Природы означает существование у нее законов и принципиальную возможность их обнаружения в конце целесообразного и трудное преодоления. Познание гармонии Природы, когда лиш нее и кажущееся отпадает, когда истина обретает вели чавую простоту и ясность, и есть высшая красота научного поиска.

Знай же, художник, что нужны во всем простота и единство.

"Красиво сведение сложности к простоте". Это принцип, видимо, является главным эстетическим принципом науки. Впрочем, вот мнение Эйнштейна: "Наш опыт убеждает нас, что Природа — это сочетание самых простых математических идей", "Бог ни за что не упустил бы возможности сделать Природу такой простой", другой выдающийся соотечественник Эйнштейна Гей-зенберг в одной из своих работ писал: "Все еще может считаться лучшим критерием корректности новых концепций старая латинская пословица "Simplex sigillum veri" ("Простота — признак истинности"), которая была выведена большими буквами в физической аудитории Геттингенского университета ".

Блестящим примером торжества простоты в науке является развитие взглядов человечества на устройство мироздания. Первой научной моделью Вселенной была геоцентрическая система великого александрийского ученого Клавдия Птолемея (II в. н. э.). Для своего времени это была красивая теория, так как она объясняла сложное и непонятное движение планет на небосводе достаточно простым образом — вращением планет вокруг Земли по основным кругам (деферентам) и вспомогательным кругам (эпициклам). Кроме того, теория Птолемея могла предсказывать положение планет на небосводе и ею с успехом пользовались мореплаватели более 1000 лет. Однако гелиоцентрическая система Николая Коперника (1473-1543) позволяла гораздо проще объяснять суть истинного Движения планет относительно неподвижных звезд, она не нуждалась в эпициклах и как более простая научная теория была более красивой [5] За многие века система Птолемея была настолько хорошо разработана, что ею продолжали пользоваться и после Коперника. Ведь система Коперника, до тех пор пока она не подверглась математической обработке и ряду уточнений,имела только мировоззренческое значение. . Законы Иоганна Кеплера (1571-1630) уточнили систему Коперника и придали ей математическую строгость, а Исаак Ньютон (1643-1727)в свою очередь показал, что законы Кеплера является логическим следствием законов механики и закона тяготения. Законы Ньютона являются вершиной красоты и простоты в научном описании Солнечной системы! А на очереди уже стоят тайны устройства Вселенной... Таким образом, эстетическая ценность науки непрерывно возрастает. Каждая новая, более простая теория воспринимается как более красивая.

Система мира по Птолемею. Иллюстрация из 'Небесного атласа' Целлариуса. Амстердам. 1708

Математика: прекрасное в науке

Согласно третьему признаку Волькенштейна, математика несет красоту в любую науку. Строго говоря, этот тезис является следствием предыдущего: красиво сведение сложности к простоте, ибо математика и есть тот инструмент науки, который позволяет, говоря словами основоположника кибернетики Норберта Винера (1894-1964), "находить порядок в хаосе, который нас окружает". Волькенштейн отмечает эту особую роль математики в науке и, следовательно, ее особую эстетическую ценность: "Математика есть область утонченной красоты. Ее формулы выражают сложные соотношение чисел в определенной форме. Поэтому они могут быть красивы, или, как говорят математики, "изящны".

Широко известно, какой эстетический восторг испытывал выдающийся немецкий физик Людвиг Больцман (1844-1906) при виде уравнений Максвелла: "Не Бог ли начертал эти письмена? " Мы позволим себе привести здесь эти уравнения без необходимых пояснений, а просто как "письмена" — красивые, но непонятные иероглифы:

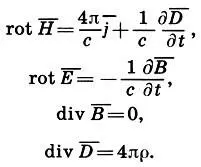
Система мира по Копернику. Иллюстрация из 'Небесного атласа' Целлариуса. По сравнению с гелиоцентрической моделью Птолемея это была более простая и более красивая научная теория.

Математика: прекрасное в науке

Что же восхищало Больцмана в этих уравнениях? Конечно, и красота формы, которую можно оценить, не понимая сути уравнений. Действительно, сами уравнения просты по форме. Части уравнений, содержащие пары 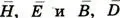, почти полностью равноправны, а сами уравнения почти полностью симметричны. Но главное, конечно, в красоте содержания уравнений, которая раскрывается далеко не каждому. Эта красота содержания заключается в том, что сами уравнения подсказали английскому физику, основателю классической электродинамики Джеймсу Клерку Максвеллу (1831 — 1879) идею электромагнитных волн и позволили связать воедино электричество, магнетизм и свет.