Александр Волошинов - Математика и искусство

Внимательно читая раздел "О красоте теорем", можно выделить три признака красоты науки , установленых Хатчесоном: 1) красота есть единство в многообразии; 2) красота заключена во всеобщности научных истин; 3) научная красота — это обретение неочевидной истины.

Принцип единства в многообразии Хатчесон считает универсальным эстетическим принципом, равно применимым и к неживой, и к живой природе, и к эстетической оценке науки. Действительно, любая математическая теорема содержит в себе бесчисленное множество истин, справедливых для каждого конкретного объекта, н0 в то же время эти конкретные истины собраны в единой общей для всех истине, устанавливаемой теоремой. Например, теорема Пифагора справедлива для бесчисленного множества конкретных прямоугольных треугольников, но все это многообразие треугольников обладает единственным общим свойством, описываемым теоремой. Вероятно, каждый школьник испытывал чувство радости, чувство научной красоты, когда впервые обнаружил, что, например, переместительное свойство сложения, замеченное им на множестве конкретных арифметических примеров, есть не что иное, как единый универсальный закон алгебры: a+b = b+a, справедливый для любых чисел.

Перейдем ко второму признаку красоты — всеобщности научных истин. "У теорем,- читаем мы у Хатчесона,- есть еще одна красота, которую нельзя обойти и которая состоит в том, что одна теорема может содержать огромное множество следствий, которые легко из нее выводятся. .. Когда исследуют природу, подобной красотой обладает познание определенных великих принципов или всеобщих сил, из которых вытекают бесчисленные следствия. Таково тяготение в схеме сэра Исаака Ньютона... И мы наслаждаемся этим удовольствием, даже если у нас нет никаких перспектив на получение какой-либо иной выгоды от такого способа Дедукции, кроме непосредственного удовольствия от созерцания красоты". Как точно сказано! И как чутко предвидит Хатчесон в 1725 г. могущество закона тяготения Ньютона, который пока еще называется "схемой Ньютона": ведь прощло только 38 лет со дня его опубликования (1687) — срок не столь уж большой для осознания столь грандиозного открытия!

Математика: прекрасное в науке

Каждый может проиллюстрировать эту мысль Хатчесона своими примерами: в математике — это любая из теорем, например теорема Пифагора, в физике — закон тяготения или законы электромагнетизма, в химии — периодический закон Менделеева, в биологии — законы генетики, всеобщность которых мы постигаем на самих себе. Возвращаясь к теореме Пифагора, заметим, что существование около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т. д.) свидетельствует об огромном числе конкретных реализаций этой теоремы и ее следствий.

Наконец, третий признак — обретение неочевидной истины. Любой из нас согласится с тем, что постижение очевидной истины (ее символом стало утверждение, что дважды два — четыре) не доставляет ему эстетического наслаждения. В аксиомах мало красоты, утверждает Хатчесон, ибо их справедливость очевидна. Немного удовольствия доставляют нам и легкие теоремы, истинность которых видна "невооруженным глазом". Только открытие истин, спрятанных от нас наукой или природой, открытие, требующее поиска и серьезных усилий, доставляет нам в конце пути истинное наслаждение — познание неведомой истины. В этом и состоит радость и красота познания. Свою мысль Хатчесон подтверждает интересным примером. Ясно, что объем цилиндра больше объема вписанного в него шара, объем которого больше объема конуса, вписанного в цилиндр. Это очевидная истина, не приносящая нам никакого удовлетворения. Но когда мы установим, что объемы этих тел относятся как 3:2:1, т. е. когда мы обретем неочевидную истину, мы почувствуем, как прекрасна эта теорема и какое мы получаем удовольствие от ее первого открытия. Напомним, что первая часть этой теоремы, связывающая объемы цилиндра и вписанной в него сферы, была доказана Архимедом и почиталась им как лучшее из всех своих замечательных открытий.

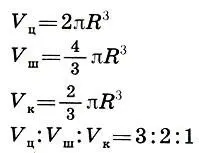
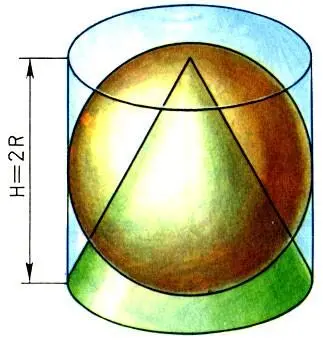
В заключение Хатчесон делает важный вывод: красота науки неравнозначна научному знанию. Красота науки заключается не в собрании застывших законов, а в обретении новых знаний, в открытии новых истин, в обнаружении стройности и порядка там, где еще недавно царил хаос. Только беспрерывное движение вперед, а точнее вверх, к новым вершинам истины,- такова формула прекрасного в науке.

Отметим еще одно существенное обстоятельство. Ясно, что все три выведенных Хатчесоном эстетических принципа справедливы для любой науки, но получены они Хатчесоном для математики. И дело здесь не в том, что остальные науки во времена Хатчесона были еще недостаточно развиты по сравнению с математикой. Дело в том, что математика во все времена была и остается "первой красавицей" среди наук и, следовательно, эстетические принципы науки наиболее ярко проявляются в математике. Чуть позже мы попытаемся обосновать эту мысль.

Хатчесон оказал заметное влияние на формирование эстетических взглядов последующих философов: Давида Юма (1711 — 1776), Адама Смита (1723-1790). Мысль Хатчесона о красоте единства в многообразии мы находим и в трудах родоначальника немецкой классической философии, "кенигсбергского затворника" [4] Кант безвыездно прожил всю свою долгую жизнь в родном Кенигсберге (ныне г. Калининград), учился в Кенигсбергском университете, затем стал его профессором, читал в нем только курсы философии, эстетики, истории, филологии, но и математики, физики, астрономии, космогонии и даже Фортификации. Всю свою жизнь этот "всеобъемлющий гений" посвятил науке, отказавшись от личной жизни и даже поездок в другие города. Иммануила Канта. В книге "Естественная история и теория неба" Кант признается в том, что космогонические проблемы для него являются не только предметом научных исследований, но и источником светлой радости. Многие строки этой книги представляют собой непревзойденные образцы вдохновенных научных стихотворений в прозе, вечный и немеркнущий сплав логики науки и поэзии искусства.

Но перенесемся из XVIII века в век XX. В 1931 г. в Москве вышла в свет небольшая книга драматурга и искусствоведа В. М. Волькенштейна "Опыт современной эстетики". Авторское введение прекрасно рисует дух того времени: "...автор ищет прежде всего определение той новой красоты, которая характеризует нашу бурную эпоху... Эта новая красота перед нами в еще невиданных произведениях искусств, в удивительных изобретениях техники, в новых методах мышления..." Последнее для нас является самым главным. Впрочем, это было отмечено и в предисловии первого наркома просвещения, писателя, искусствоведа, академика А. В. Луначарского (1875-1933), которым открывалась книга: "Само оглавление книги показывает, что Волькенштейн стремится распространить понятия эстетического на область мышления, считая возможным оценивать с эстетической точки зрения понятия: математические, физические, шахматную игру, всякое научное построение или формулу. Не подлежит сомнению, что это так. Беспрестанно у самих ученых... с уст срываются замечания: красивая теория, изящное разрешение затруднений и т. д. и т. д. Восхищение перед силой человеческого ума есть, конечно, глубоко эстетическое явление, своеобразное, но ничем радикально не различающееся от восхищения перед физической ловкостью человека, перед красотою здания и т. д.".