Джо Боулер - Математическое мышление
- Название:Математическое мышление
- Автор:
- Жанр:
- Издательство:Манн, Иванов и Фербер
- Год:2019
- Город:Москва
- ISBN:9785001008910
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Джо Боулер - Математическое мышление краткое содержание
Математическое мышление - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Stigler J., Hiebert J. The teaching gap: Best ideas from the world’s teachers for improving education in the classroom. New York: Free Press, 1999.
Stipek D. J. Motivation to learn: Integrating theory and practice. New York: Pearson, 1993.
Supekar K., Swigart A. G., Tenison C. et al. Neural predictors of individual differences in response to math tutoring in primary-grade school children // Proceedings of the National Academy of Sciences. 2013. Vol. 110 (20). Pp. 8230–8235.
Thompson G. Teaching the brain to learn // THE Journal, 2014, June 2 // http://thejournal.com/articles/2014/06/02/teaching-the-brain-to-learn.aspx.
Thurston W. Mathematical education // Notices of the American Mathematical Society. 1990. Vol. 37 (7). Pp. 844–850.
Tobias S. Overcoming math anxiety. New York: Norton, 1978.
Treisman U. Studying students studying calculus: A look at the lives of minority mathematics students in college // College Mathematics Journal. 1992. Vol. 23 (5). Pp. 362–372.
Vélez W. Y., Maxwell J. W., Rose C. Report on the 2012–2013 new doctoral recipients // Notices of the American Mathematical Society. 2013. Vol. 61 (8). Pp. 874–884.
Wang J. Opportunity to learn: The impacts and policy implications // Educational Evaluation and Policy Analysis. 1998. Vol. 20 (3). Pp. 137–156 // doi: 10.3102/01623737020003137.
Wenger E. Communities of practice: Learning, meaning and identity. Cambridge: Cambridge University Press, 1998.
White B. Y., Frederiksen J. R. Inquiry, modeling, and metacognition: Making science accessible to all students // Cognition and Instruction. 1998. Vol. 16 (1). Pp. 3–118.
Wolfram C. Teaching kids real math with computers. TED Talks, 2010, July // http://www.ted.com/talks/conrad_wolfram_teaching_kids_real_math_with_computers?language=en.
Woollett K., Maguire E.A. Acquiring “The Knowledge” of London’s layout drives structural brain changes // Current Biology. 2011. Vol. 21 (24). Pp. 2109–2114.
YouCubed at Stanford University. Making groupwork equal. Stanford Graduate School of Education, 2015a // http://www.youcubed.org/category/making-group-work-equal.
YouCubed at Stanford University. Moving colors. Stanford Graduate School of Education, 2015b // http://www.youcubed.org/task/moving-colors.
YouCubed at Stanford University. Tour of mathematical connections. Stanford Graduate School of Education, 2015c // http://www.youcubed.org/tour-of-mathematical-connections.
YouCubed at Stanford University. Video: High-quality teaching examples. Stanford Graduate School of Education, 2015d // www.youcubed.org/high-quality-teaching-examples/.
Zaleski A. Western High School’s RoboDoves crushes the competition, stereotypes. Baltimore Sun, 2014, November 12 // http://www.baltimoresun.com/entertainment/bthesite/bs-b-1113-cover-robodoves-20141111-story.html#page=1.
Zohar A., Sela D. Her physics, his physics: Gender issues in Israeli advanced placement physics classes // International Journal of Science Education. 2003. Vol. 25 (2). P. 261.
Приложение
Вопросы для размышлений: домашнее задание по математике
Задача с фигурами
Задача с палочками Кюизенера
Треугольник Паскаля
Задача на отрицательное пространство
Найдите четырехугольники!
Четыре четверки
Информационный бюллетень
Прыжки в длину
Параллельные прямые и секущая
Лестница
Складывание бумаги
Конус и цилиндр
Моя домашняя работа, мои размышления
Сортировка чисел
Растущие прямоугольники
Задача на линейную функцию
Задача на математическую функцию
Шнурки
Распределение ролей в группе — США
Распределение ролей в группе — Великобритания
Самооценка: многоугольники
Алгебра 1. Самооценка
Две звезды и пожелание
Размышления
Мозаичная задача А по алгебре
Мозаичная задача Б по алгебре
Мозаичная задача В по алгебре
Мозаичная задача Г по алгебре
Билет на выход
Самооценка «Покажите, что вы можете сделать»
Математические цели оценки участия в работе группы
Групповые цели оценки участия в работе группы
Собачьи галеты
Акцент на математических связях
Цветовое кодирование шоколадного пирога
Раскрашенный куб
Привязанный козлик
Моделирование распределения мирового богатства
Футбольный вратарь
Мы хотели бы знать
Вопросы для размышлений: домашнее задание по математикеЧасть 1: вопросы, требующие письменного ответа
* Ответ на вопрос(ы) должен быть очень подробным! Пожалуйста, используйте полные предложения и будьте готовы сформулировать свой ответ на уроке на следующий день.
1. Какие основные математические концепции или идеи вы изучили сегодня или что вы обсуждали на уроке сегодня? _____
2. Какие вопросы у вас остались по поводу _____? Если у вас нет вопросов, запишите аналогичную задачу и решите ее.
3. Опишите ошибку или заблуждение, которые возникли у вас или у кого-то из одноклассников сегодня на уроке. Что вы узнали благодаря этому?
__________
4. Какой подход вы или ваша группа использовали для решения задачи или нескольких задач? Был ли ваш подход эффективным? Какой урок вы извлекли из этого подхода?
5. Подробно опишите алгоритм решения этой задачи, который использовал на уроке кто-то другой. Чем он был похож на ваш и чем отличался от него?
__________
6. Какие новые слова или термины были представлены сегодня? Что, по вашему мнению, означает каждое новое слово? Приведите пример каждого слова (или нарисуйте то, что оно означает). _____
7. Вокруг чего развернулась самая серьезная математическая дискуссия на уроке сегодня? Что вы узнали из нее? _____
8. В чем сходство или различие между _____ и _____?
9. Что произошло бы, если бы вы изменили _____?
10. В чем были ваши сильные и слабые места в работе над этой темой? Как вы планируете исправить слабые места? _____
Материал предоставлен Екатериной Мильвидской и Тианой Тебельман на условиях лицензии Creative Commons Attribution 3.0.
Задача с фигурамиКак вы представляете себе рост фигур?

Источник: предоставлено Рут Паркер; задача используется в рамках курсов MEC (Mathematics Education Collaborative).
Последовательности палочек КюизенераОпределите, сколько разных последовательностей можно составить для палочек любой длины. Например, для светло-зеленой палочки можно составить 4 последовательности:
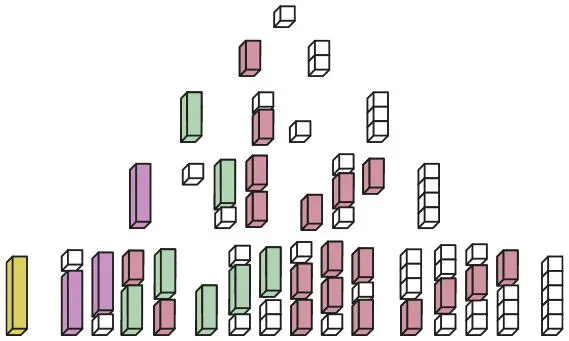
Источник: предоставлено Рут Паркер; задача используется в рамках курсов MEC (Mathematics Education Collaborative).
Треугольник Паскаля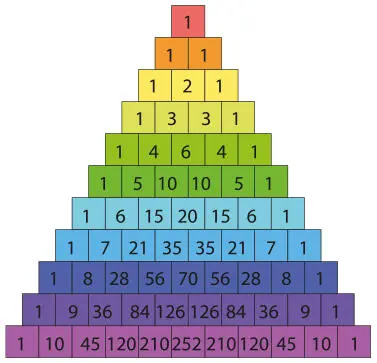 Задача на отрицательное пространство
Задача на отрицательное пространство
1. Как выглядел бы рисунок 100?
2. Представьте себе, что вы могли бы продолжить построение этой модели в обратном направлении. Сколько ячеек было бы на рисунке –1? (Да, рисунок –1, что бы это ни значило!)
3. Как выглядел бы рисунок –1?
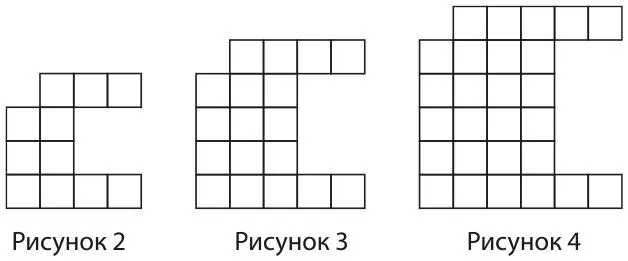
Источник: на основе материалов, предоставленных Карлосом Кабана.
Найдите четырехугольники!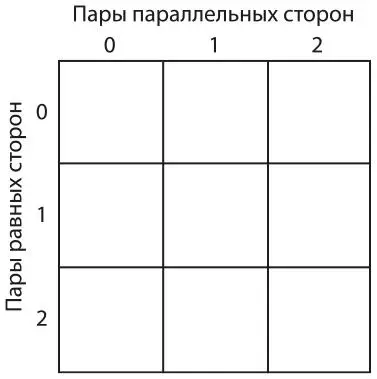 Четыре четверки
Четыре четверки
Можете ли вы найти все числа от 1 до 20, используя только числа 4 и любые математические операции?
Дополнительные вопросы
Можете ли вы найти несколько способов составления каждого числа из четырех четверок?
Можете ли вы составить таким образом число больше 20?
Можете ли вы найти отрицательные целые числа с помощью четырех четверок?
Читать дальшеИнтервал:
Закладка:





![Джоан Дидион - Год магического мышления [litres с оптимизированной обложкой]](/books/1145878/dzhoan-didion-god-magicheskogo-myshleniya-litres-s-op.webp)




