Роман Душкин - Математика и криптография : тайны шифров и логическое мышление

Теперь предлагаю изучить один очень занятный метод стеганографии (и криптографии одновременно). Этот метод переворачивает сознание у тех, кто впервые о нём узнаёт, хотя, по сути, он очень прост. Но переворот сознания необходим тем, кто старается познать тайны криптографии, поэтому мы должны рассмотреть этот метод.

Что такое стеганография? Это набор методов и практик сокрытия сообщений. Основная цель стеганографии заключается в том, чтобы скрыть сам факт передачи тайного сообщения. Другими словами, тайное сообщение как бы прячется. Оно даже может быть не шифрованным. Но если спрятанное сообщение ещё и зашифровать каким-нибудь способом, то степень защиты будет повышена, особенно если метод шифрования нарушает частоты распределения символов в шифруемом тексте. Тогда найти стеганограмму намного сложнее, поскольку она начинает выглядеть как «шум». Непосвящённый человек не сможет выявить её, а у криптоаналитика будет очень мало зацепок, чтобы попытаться обнаружить стеганограмму (например, статистическими методами).

В течение третьей недели мы научимся скрывать сообщение методом, который придумал английский философ и математик Фрэнсис Бэкон. Мы немного изменим его метод и применим его для русского языка. В итоге получится очень интересная вещь, которой можно пользоваться в любых областях жизни. Начнём же…

Помните, я не зря упомянул о том, что в нашем новом алфавите ровно тридцать два символа. Число 32 для криптографов и математиков — «круглое», поскольку в двоичной системе счисления записывается как «100000». Другими словами, для представления тридцати двух символов нам требуется 5 бит информации, поскольку 32 = 2 5. Мы можем воспользоваться этим для нового способа кодирования символов нашего алфавита:

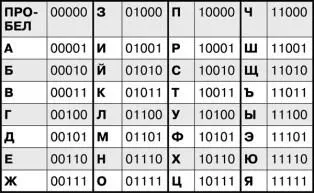
Тот из читателей, кто изощрён в информатике или программировании, уже понял, что это двоичный код для всех тридцати двух символов. Другими словами, каждому символу из алфавита ставится в соответствие пятизначное двоичное число, то есть число, состоящее ровно из пяти цифр 0 или 1. При этом нули на первых местах не удаляются, как мы это привыкли делать в десятичной системе. Здесь особенно важно, чтобы длина кода для каждого символа была равна пяти.

Соответственно, чтобы зашифровать текст, необходимо выписать один за другим код каждого символа. Например, пусть есть текст «ПОДГОТОВЬ ИНГРЕДИЕНТЫ К МОЕМУ ПРИЕЗДУ». Этот текст шифруется при помощи представленного выше кода так:

10000011110010100100011111001101111000111101100000010010111000100100010011000101 01001001100111010011111000000001011000000110101111001100110110100000001000010001 0100100110010000010110100

Атепер ь самое гл авн ое. П устьциф ра0 обознач аетоб ычную бук ву, ац ифра 1 — жир ную. Вес ьэтот ко дм ожн о«н анес ти»н апр оизвольный тек ст при помощ ита ко госоот ветс тви я.И, самое гл авное, нео бя зат ель ноис пользо ва тьс войство жирности символа, для этих целей подойдёт любое двоичное свойство: большая буква или маленькая буква, прямая или курсив, красного цвета или чёрного. Можно даже использовать такие свойства, как «находится в первой половине алфавита или во второй» или «находится на чётном месте в алфавите или на нечётном». Но эти два последних свойства сложнее, при помощи их спрятать код можно не в любом тексте.

Как видно, эта же шифрограмма «нанесена» на обычные слова в начале предыдущего абзаца, при этом использовались все символы для нанесения (то есть и цифры, и знаки препинания). Неподготовленный читатель даже не обратит внимания на такое странное начертание текста. Но грамотный криптоаналитик, конечно же, всё сразу поймёт, этим никого не удивишь. Поэтому обычно используют более тонкие свойства, которые не так тривиальны и не видны невооружённым глазом.

Таким образом, на третьей неделе обучения надо составить и написать письмо, шифрограмма в котором будет скрыта. При составлении текста, подлежащего сокрытию, необходимо иметь в виду, что для его кодирования с помощью жирных начертаний требуется в пять раз больше символов. Я рекомендовал бы написать обычное письмо, в тексте которого не ведётся речь о шифровании вообще. А вот в скрываемом тексте можно использовать какие-нибудь нравоучения на тему, как хорошо знать и уметь заниматься шифрованием и дешифровкой.

Необходимо быть крайне внимательным при кодировании текста. Нет ничего страшного в том, что в каком-нибудь одном месте будет изменён один бит (0 на 1 или 1 на 0), поскольку это всего лишь приведёт к появлению единичной ошибки в дешифрованном открытом тексте. Намного хуже будет, если в какой-то момент будет пропущен бит. Это приведёт к сдвигу, в результате которого после расшифровки получится бессмыслица. Нет, в конце концов, её тоже можно будет расшифровать, поскольку это будет довольно структурированная бессмыслица. Но её вид вызовет у ребёнка недоумение, поскольку он подумает, что идёт по неправильному пути.

Поэтому я рекомендую воспользоваться компьютером, чтобы подготовить и затем проверить кодирование скрытого текста. Затем можно будет перенести его в письмо, которое, как мы договорились, лучше писать от руки. Соответственно, при кодировании скрытого текста надо внимательно относиться к жирности букв, поскольку для образовательных целей нужно, чтобы два состояния символов отличались друг от друга.

Четвёртая неделя знаменуется изучением важнейшей для криптографии математической операции, которая называется «Исключающее ИЛИ» и обозначается символом «⊕». Эта операция работает на битах: на вход она принимает два бита, а возвращает один. В результате получается значение 0 тогда, когда оба входных бита одинаковы, и 1, когда входные биты различны. Другими словами, таблица истинности этой операции выглядит следующим образом:

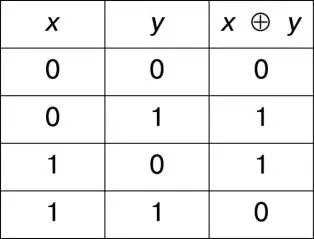
Эта операция обладает одним важным свойством. Если повторно применить эту операцию с тем же самым вторым операндом к одному биту, то в результате вернется первоначальное значение этого бита. Другими словами: ( x ⊕ y) ⊕ y = x Это свойство вытекает из ассоциативности операции и того наблюдения, что её применение к двум одинаковым значениям всегда возвращает 0, каким бы ни были эти значения, а если применить эту операцию с некоторым битом и нулём, то в результате получится этот бит. То есть: ( x ⊕ y ) ⊕ y = x ⊕ ( y ⊕ y ) = x ⊕ 0 = x .