Роман Душкин - Криптографические приключения: таинственные шифры и математические задачи

На следующий день папа прямо с самого утра продолжил занятия. Он сказал, что сегодня мы будем заниматься весь день, до обеда он расскажет нам теорию, а во второй половине дня мы займёмся практикой. Я с нетерпением поглядывал на лазерные пушки, которые мы настроили вчера.

Рассевшись, мы начали занятие. Папа взял с места в карьер:

— Давайте подумаем, что мы знаем о свете. Вы же помните, что лазер — это свет, пучок мельчайших частиц света, называемых «фотонами»?

Мы дружно кивнули. Он продолжил:

— Для передачи информации мы воспользуемся характеристикой фотона, которая называется поляризацией. Эта характеристика обозначает то, в какой плоскости колеблется фотон. Для наших целей мы возьмём четыре способа поляризации фотона: горизонтальный, вертикальный и два диагональных — слева направо и справа налево. Четыре способа, понятно? Вас ничего не смущает?

Катя сразу же нашлась:

— Но мы же раньше говорили, что для передачи любой информации можно пользоваться битами, то есть 0 и 1. Другими словами, нам нужно два разных значения характеристики фотона. Зачем же мы берём четыре?

— Вопрос резонный, именно его я и хотел услышать. Но в этом и состоит суть алгоритма. Дело в том, что поляризацию фотона можно измерять двумя способами: во-первых, в вертикально-горизонтальном направлении, а во-вторых — в диагонально-диагональном. Первый способ измерения обозначается прямым крестом, а второй — косым.

Папа нарисовал в пыли на земле две фигуры:

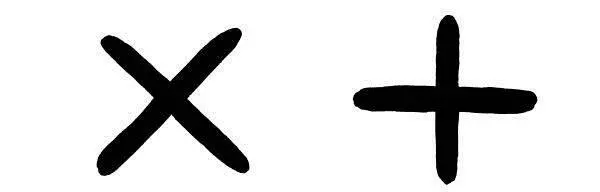
Он продолжил:

— И вот что интересно. Если фотон поляризован вертикально или горизонтально, то измеряя его в вертикально-горизонтальном направлении, прибор даст точную поляризацию. А если измерять в диагонально-диагональном направлении, то прибор с вероятностью 50 % покажет поляризацию слева направо или справа налево, независимо от того, какая она была у фотона. То же самое касается и измерения диагонально поляризованных фотонов при помощи вертикально-горизонтального прибора: в половине случаев прибор покажет вертикальную поляризацию, в половине — горизонтальную, причём опять независимо от того, какая поляризация была у фотона изначально. Понятно?

Мы с Катей одновременно помотали головами. Папа вздохнул и нарисовал на листке такую схему:

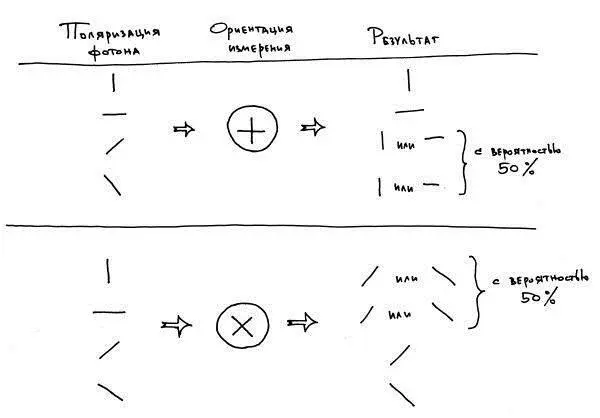
Да, так стало намного понятнее. Тем временем папа продолжил:

— Но эти мои слова не объясняют, зачем нам четыре разных варианта фотона, ведь так? Действительно, это была лишь присказка. Слушайте сказку…

И папа рассказал нам удивительные вещи. Оказалось, что четыре возможных состояния фотона всё равно кодируют два бита, просто используется некоторая избыточность. Бит 0 представляется двумя способами: вертикальная поляризация и поляризация слева направо. Соответственно, бит 1 представляется в виде горизонтальной поляризации и поляризации справа-налево.

Когда некто хочет передать своему товарищу секретный ключ, он создает случайную последовательность битов. Однако потом он создает вторую случайную последовательность, которая определяет, в какой поляризации передавать соответствующий бит. При этом «0» в этой второй последовательности обозначает вертикально-горизонтальную поляризацию, а «1» — диагонально-диагональную. Получается примерно так:

Соответственно, теперь эту последовательность фотонов нужно отправить второму участнику переписки: \/—||/—/\|. Но что же должен сделать он? Он же не знает, в какой именно поляризации отправлены фотоны, так что измерять он может любым из двух приборов: вертикально-горизонтальным или диагонально-диагональным. Для измерения можно выбрать один прибор, либо использовать для каждого прибора свой прибор, выбираемый случайным образом. Это абсолютно неважно, так как в среднем половина переданных фотонов будет измерена правильным прибором, а другая половина неправильным, и результат неправильного измерения случаен.

Например, пусть для указанной передачи получатель использовал вертикально-горизонтальный прибор. Тогда он мог получить такой результат: ||—||—|—|. Это соответствует последовательности битов 0010011010. А передана была 0110011100. Как же быть? Всё просто. Теперь отправитель связывается с получателем по открытому каналу — например, по телефону — и говорит, в какой поляризации были отправлены фотоны, а получатель сообщает, какие из них были измерены правильным образом. В нашем примере получается, что правильно были измерены только третий, четвёртый, пятый, седьмой и десятый фотоны, и именно их надо оставить, а неправильно измеренные фотоны выкинуть. И тогда получается двоичное число 10010, одинаковое и у отправителя, и у получателя. Это число и есть секретный ключ, который после передачи можно использовать для шифрования информации при помощи, например, одноразового блокнота.

Всё это было понятно. Папа попросил нас с Катей передать друг другу несколько последовательностей битов, записывая их на клочках бумаги, и мы немного потренировались. Проблем не возникало, мы получали одинаковые последовательности после вычёркивания неправильно измеренных битов. Тогда Катя спросила:

— Но всё равно непонятно, зачем четыре разных фотона? Ведь мы всё равно передаём биты.

Папа кивнул и сказал:

— Вот в этом-то суть метода. Это позволяет противостоять атаке «человек посередине». Вот смотрите. Некто перехватывает фотоны, посылаемые отправителем, и измеряет их. Но он же тоже не знает, в какой поляризации они посланы, а потому примерно половина фотонов будет измерена неправильно. А этот некто должен послать измеренный фотон дальше, чтобы у получателя не появилось подозрений, что их перехватывают. Если фотон измерен неверно и при этом злоумышленник даже не понимает, какие фотоны он измерил неверно, то он не сможет корректно передать данные. И отправитель с получателем смогут определить, что передача была скомпрометирована. Понятно?

Вроде бы интуитивно это было понятно, но всё равно надо проверить. Я попросил папу привести нам пример. Тогда он вновь нарисовал предыдущую таблицу, но добавил к ней три новые строки:

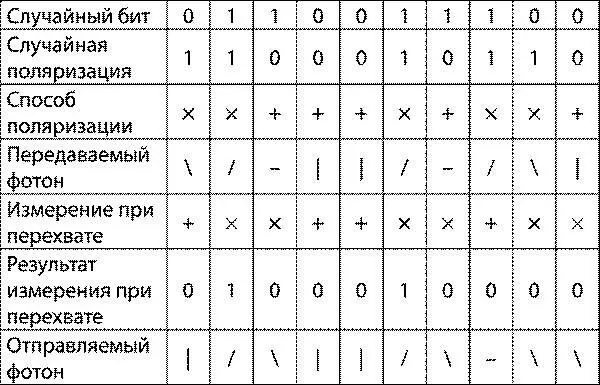
Второй участник переписки получает последовательность фотонов: |/\||/\ — \\. Он опять не знает, в какой поляризации их измерять, а потому измеряет случайным образом. На самом деле опять можно использовать только один прибор для измерения. Пусть, как и в прошлый раз, получатель измерил все фотоны вертикально-горизонтальным прибором. Он прочитает что-то типа такого: |—|||—|—. Это соответствует последовательности битов 0110001101. А передана была 0110011100. Как и в прошлый раз, получатель обращается к отправителю по открытому каналу и узнаёт, какие биты он измерил правильно. Как и в прошлый раз, правильно он измерил третий, четвёртый, пятый, седьмой и десятый фотоны, а потому остаются только эти биты. На стороне отправителя последовательность выглядит как 1001 0, а на стороне получателя 1001 1. Как видно, десятый бит пришёл с ошибкой — и злоумышленнику-перехватчику ещё повезло, что с ошибкой пришёл только один бит, поскольку в среднем ошибочными будет половина битов из оставшихся.