Алексей Куприн - Слово о карте

Одной из основных характеристик аэрофотоснимка является его масштаб. Отчего же он зависит? Во-первых, от высоты фотографирования. С малых высот получают крупномасштабные аэрофотоснимки, а чем больше высота съемки, тем масштаб снимка мельче. Тем не менее с таким ответом согласиться нельзя. Взгляните на рис. 51, где показана схема воздушного фотографирования.

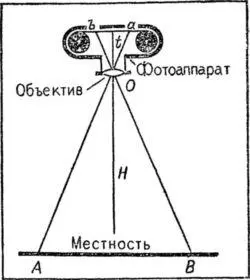
Рис. 51. Схема воздушного фотографирования.

Лучи от точек местности А и В проходят через центр объектива О и попадают на пленку соответственно в точках а и Ь . Из подобия треугольников АВО и аЬО можно вывести следующую зависимость: аЬ / АВ = f/Н .

Отношение ab / AB и есть масштаб фотографирования. Он обычно выражается в виде дроби, числителем которой будет единица, а знаменателем — число, показывающее, во сколько раз размеры на карте или аэроснимке меньше соответствующих размеров на местности. А что же представляют собой обозначения f и H ? Буквой f обозначено расстояние от объектива до пленки. Кто знаком с фотографированием, тот знает, что его называют фокусным расстоянием фотоаппарата. Что касается второй величины, обозначенной буквой H , то это и есть высота съемки. Значит, масштаб аэроснимка зависит не только от высоты фотографирования, но и от фокусного расстояния фотоаппарата. Чтобы убедиться в этом, решим задачу. Съемка выполнена в первом случае с самолета, пролетавшего на высоте 12 км , фотоаппаратом с фокусным расстоянием 0,2 м , а во втором случае — со спутника, удаленного от Земли на 150 км , фотоаппаратом с фокусным расстоянием 3 м . В каком случае масштаб аэрофотоснимка будет более крупным?

Подставив исходные данные в формулу, в первом случае получим

1/ m = 0,2/12 000 = 1/60 000,

а во втором

1/ m = 3/150 000 = 1/50 000.

Как видите, масштаб аэроснимка во втором случае получился крупнее, несмотря на то, что высота фотографирования была значительно большей.

На первый взгляд кажется, что по аэрофотоснимкам можно легко создать карту. Однако это процесс сложный, состоящий из множества операций. Прежде всего аэрофотоснимки нужно привязать к опорным пунктам, координаты которых определены геодезическими измерениями с высокой точностью. Сеть опорных пунктов — это геометрическое обоснование карты, своего рода ее каркас. Любая точка, изображенная на аэрофотоснимке, занимает строго определенное положение относительно опорных пунктов. Во-вторых, аэрофотоснимки по своим измерительным свойствам отличаются от карты, так как на них местность изображается в центральной проекции, а не в ортогональной, как на топографической карте.

В центральной проекции изображение на плоскости получается путем проектирования земной поверхности из одной точки — центра проекции. В этом случае полное подобие изображения с местностью может быть только при условии, что плоскость, на которой получается изображение, строго параллельна фотографируемой поверхности. В действительности это случается весьма редко.

Из-за колебаний самолета в полете оптическая ось аэрофотоаппарата отклоняется от вертикального положения, и поэтому фотографирование производится под некоторым углом. Кроме того, фотографируемая местность не является ровной горизонтальной плоскостью, а имеет рельеф. Вследствие указанных причин изображения контуров местности на аэроснимке получаются искаженными, т. е. смещенными от того положения, которое они должны занимать на карте. Поэтому, прежде чем превратиться в карту, аэроснимки проходят обработку на различных приборах.

Люди определили размеры нашей планеты, измерили площади стран, высоты поверхностей горных вершин, глубины морей и океанов, построили города, каналы и дороги, проложили путь в межпланетное пространство кораблей. Каждое из этих достижений человеческого разума не обошлось без широкого применения одной из древнейших наук о Земле — геодезии, что в переводе с греческого означает «землеизмерение».

Карта Земли также не могла быть составлена без длительной и кропотливой работы геодезистов, определявших шаг за шагом на протяжении многих лет координаты опорных пунктов на земной поверхности. Эти пункты, нанесенные по координатам на сетку параллелей и меридианов, представляют съемочное обоснование, позволяющее определять по карте точное положение любого земного объекта.

Географические координаты геодезисты определяют по звездам с помощью высокоточных астрономических приборов, а вычисления производят по довольно сложным формулам. Раньше решать эту задачу было намного труднее: широту определяли приблизительно по высоте Полярной звезды, а вот с долготой дело обстояло совсем плохо. Чтобы узнать долготу места, скажем, Пулково, где помещается главная обсерватория нашей страны, по отношению к Гринвичу, через который проходит нулевой меридиан, нужно точно знать, на сколько часов, минут и секунд разнится местное время этих пунктов. Сейчас это сделать легко: есть очень точные часы, есть радио. А всего сто с небольшим лет назад для того, чтобы сравнить пулковское время с гринвичским, пришлось снаряжать морскую экспедицию из нескольких кораблей, на которых везли 81 хронометр!

Астрономические наблюдения, с помощью которых определяют местоположение пунктов на земной поверхности, очень громоздки и требуют больших затрат времени. В 1614 г, голландский астроном В. Снеллиус предложил очень простой и точный способ определения опорных точек, который получил название триангуляции. Достаточно иметь всего два астрономических пункта А и В (рис. 52), и от них по измеренным углам α и β треугольника можно получить третий пункт С ; от третьего и одного исходного пункта — четвертый D и т. д.

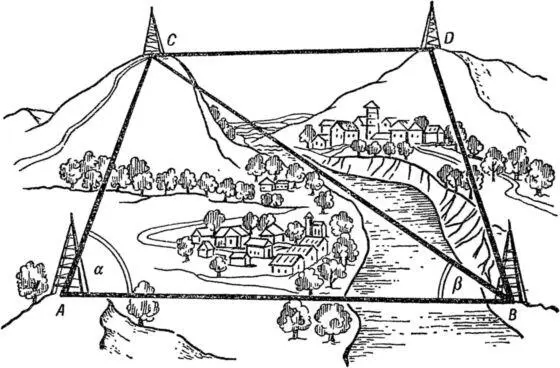
Рис. 52. Схема триангуляции .

Так, переходя от одного видимого издалека пункта к другому, можно покрыть треугольниками громадную полосу на поверхности Земли — вдоль любого меридиана или параллели — и вычислить длину этих отрезков градусной сетки.

Достоинство триангуляции состоит в том, что она сокращает до минимума трудоемкие линейные измерения, которые сводятся к определению лишь одной стороны — базиса, правда, измеряют его с величайшей точностью и тщательностью. Углы воображаемых треугольников измеряют угломерным прибором — теодолитом. В зрительную трубу теодолита вначале наблюдают одну вершину треугольника, потом другую и затем по горизонтальному кругу прибора отсчитывают величину угла.