Алексей Куприн - Слово о карте

Прежде всего определим площадь живого сечения каждой реки. Нам известно, что все реки, как правило, имеют постепенное увеличение глубины. Для приближенных расчетов можно считать, что указанная на карте глубина проходит не по всему участку поперечного сечения, а только по половине его. Таким образом, живое сечение реки имеет форму трапеции, площадь которой, как известно, равна произведению полусуммы оснований на высоту. Для реки Шуя трапеция имеет основания 40 и 20 м, и высоту 1,5 м, следовательно ее площадь составит [(40+20)/2]1,5 = 45 м 2. Для реки Сан размеры трапеции равны соответственно 60, 30 и 1,0 м; площадь ее равна [(60+30)/2]1,0 = 45 м 2.

Такое количество воды проносилось бы в каждой реке ежесекундно, если бы скорость течения составляла 1 м/с . В нашем случае река Шуя имеет скорость течения 2 м/с, а река Сан — 0,5 м/с. Значит, расход воды за 1 с в реке Шуя составит 90 м 3, а в реке Сан — всего 22,5 м 3, т. е. в 4 раза меньше.

Очень много интересных задач можно решать и по горизонталям, которые отображают рельеф местности на топографических картах. Даже простой овал одной горизонтали с бергштрихом может рассказать о многом: о том, что это форма рельефа суши и что эта форма положительная, о ее ориентировке в пространстве, высоте над уровнем моря, очертаниях к размерах. Если дополнить этот простой рисунок одной-двумя горизонталями, проходящими на известной высоте, то это позволит определить по карте высоту и направление уже более крупной формы земной поверхности, крутизну и направление ее склонов, а также абсолютные высоты и относительные превышения любых точек местности в пределах площади, оконтуренной нижней горизонталью.

Горизонталь — это след сечения земной поверхности горизонтальной плоскостью. А если земную поверхность пересечь вертикальной плоскостью, то в результате получится профиль рельефа местности.

Профили можно строить не только по прямым линиям, но и по любым кривым, например по дорогам, как это показано на рис. 43, а.

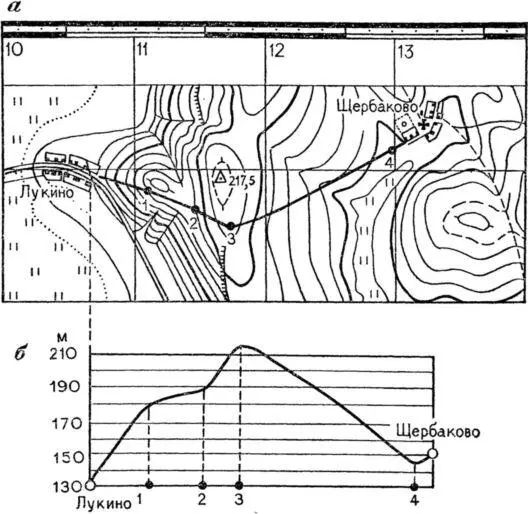
Рис. 43. Профиль рельефа вдоль дороги .

Для его построения на бумаге прочертим ряд параллельных линий, равных по длине протяженности дороги в масштабе карты (рис. 43, б). Расстояние между ними, соответствующее высоте сечения, берется равным 3–5 мм, а число линий равно числу горизонталей на данном участке, не считая равнозначных. Слева у параллельных линий подпишем отметки горизонталей, при этом меньшая по величине отметка должна быть внизу. Затем на карте по дороге наметим перегибы скатов (в нашем примере точки № 1, 2, 3, 4) и перенесем их на нижнюю линию. На исходном и конечном пунктах, а также на точках перегибов скатов определим по карте их абсолютные высоты. Они получились равными: окраина Лукино —130 м, № 1 — 180 м, № 2 — 190 м, № 3 — 212 м, № 4 — 145 м, окраина Щербакове — 150 м. От этих точек, перенесенных с карты на нижнюю линию чертежа, восставим перпендикуляры до пересечения с соответствующими по отметкам параллельными линиями. Точки пересечения соединим плавной линией и получим профиль нашего пути, который учитывает все неровности рельефа. В то же время он условный, так как вертикальные размеры на кем значительно больше, нежели полагалось бы по масштабу карты.

Если нужно представить вид земной поверхности с какой-либо точки, можно построить силуэт местности. Как это делается, видно на рис. 44.

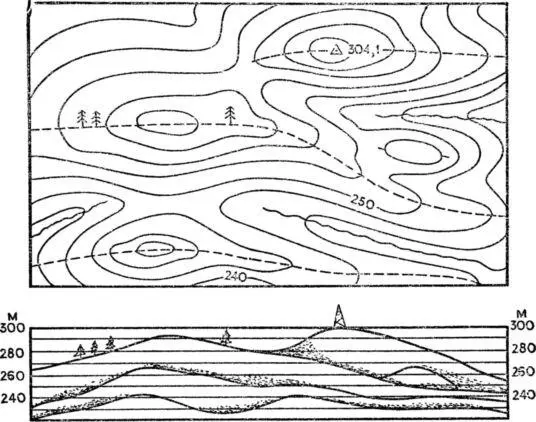
Рис. 44. Силуэт местности .

Вначале находят все водораздельные линии и на каждую из них строят профиль. Изображают при этом только те части профиля, которые не закрываются впереди лежащими возвышенностями.

Очень наглядно и вместе с тем достаточно точно рельеф какого-либо участка изображается на блок-диаграмме, которую нетрудно составить по топографической карте (рис. 45).

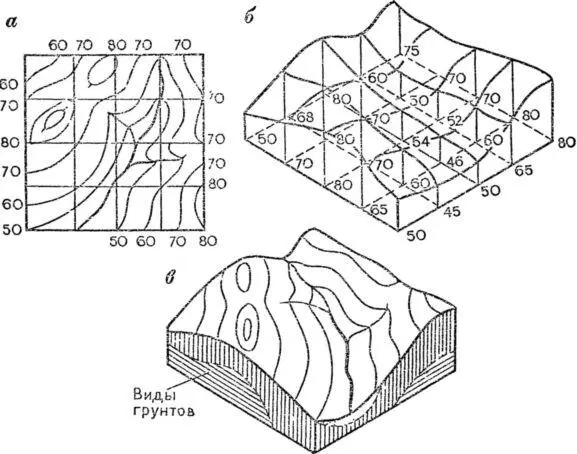
Рис. 45. Блок-диаграмма .

Блок-диаграмма — это трехмерный рисунок, совмещающий перспективное изображение поверхности и профили по двум взаимно перпендикулярным направлениям. Благодаря своей наглядности и трехмерности такие чертежи позволяют лучше представить взаимосвязи между явлениями, произвести измерения и сопоставления. По профильным плоскостям показывают обычно какую-либо геологическую структуру — виды грунтов, распределение вечной мерзлоты, грунтовых вод и др.

Блок-диаграмма строится в аксонометрической проекции, у которой оси располагаются под углом 120° друг к другу. Прежде всего трансформируем квадратную сетку топографической карты (рис. 45, а), направив ее стороны по горизонтальным аксонометрическим осям (рис. 45, б). Длины сторон при этом сохраняются неизменными. Затем у вершин каждой клетки выписываем абсолютные высоты, определенные по карте, и их значения в выбранном масштабе откладываем вдоль вертикальной оси. Соединив вершины отложенных отрезков, получим сетку квадратов в аксонометрической проекции. На эту сетку переносим с карты по клеткам горизонтали, реки и другие объекты. Подписи высот сотрем; на профильные грани нанесем геологические данные, и блок-диаграмма готова (рис. 45, в).

Масштабы вдоль боковых граней блок-диаграммы остаются теми же, что и на карте, а по вертикали масштаб равен масштабу профиля. Это позволяет проводить измерения на полученной модели в любых направлениях. Само же название «аксонометрия» означает «осеметрия», т. е. возможность вести измерения вдоль осей.

Если две поверхности, изображенные горизонталями на картах одного и того же масштаба, совместить, то можно произвести простейшие арифметические действия: слежение или вычитание рельефа поверхностей. При этом получится новая карта с изолиниями сумм или разностей. Задача сложения поверхностей может возникнуть, например, при подсчете мощности различных отложений. Вычитание одной поверхности из другой применяется при подсчете объема снесенного и отложенного материала, при определении поверхности стока воды и в других случаях.

Пусть требуется суммировать поверхности А и Б (рис. 46, а).

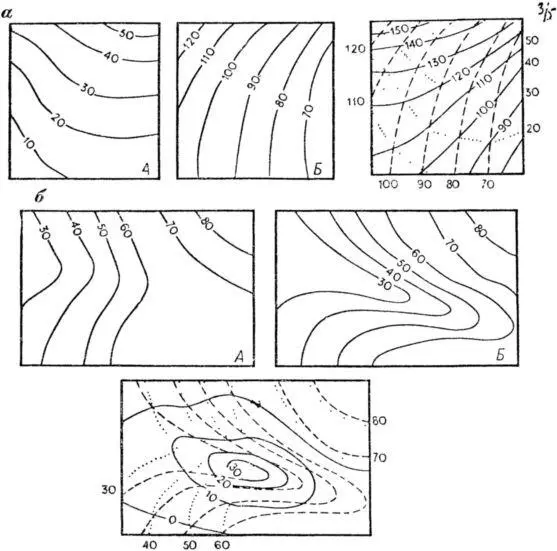
Рис. 46. Сложение и вычитание поверхностей .

Совместим обе карты. В точках пересечения изолиний определим суммы, и по ним проведем изолинии сумм А + Б . Легко заметить, что изолинии сумм обычно проходят по диагоналям четырехугольников, образованных пересекающимися изолиниями слагающих поверхностей. Это избавляет от обязательного суммирования значений в каждом пересечении и позволяет проводить изолинии сумм механически.