Алексей Куприн - Слово о карте

Очень удобно определять площадь по сетке квадратов, нанесенной на прозрачную бумагу или пленку. Стороны квадратов должны быть такими, чтобы каждый из них соответствовал целому числу гектаров или квадратных километров. Так, для карт масштабов 1:25 000, 1:250 000 и 1:2 500 000 квадрат вычерчивают со стороной 4 мм. Для первой карты один квадрат будет соответствовать 1 га , для второй — 1 км 2и для третьей — 100 км 2. Накладывая такую сетку на карту, подсчитывают число квадратов, покрывающих площадь, причем доли квадратов определяют на глаз.

Вместо сетки квадратов можно ограничиться только точками, отмеченными в вершинах квадратов (рис. 38, б). Количество точек в пределах контура будет соответствовать числу квадратов, и здесь уже не нужно подсчитывать число долей квадратов. В нашем случае на изображение контура попало 45 точек, значит, площадь, заключенная в нем, составляет 45 км 2.

Для точного измерения площадей применяют специальный прибор — планиметр. Простейший планиметр-топорик можно легко изготовить самому. Он состоит из металлического стержня, согнутого в виде широкой буквы П (рис. 39).

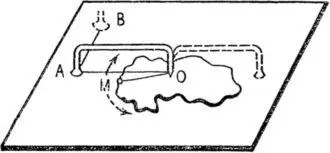
Рис. 39. Схема измерения площади планиметром-топориком .

Один конец инструмента расплющивается в виде топорика, а другой — ведущий конец заостряется в иглу. Для правильного измерения площади необходимо, чтобы острие иглы лежало в плоскости, проходящей через лезвие топорика; во время работы инструмент должен быть в вертикальном положении.

Для определения площади какой-либо фигуры намечают на глаз ее центр тяжести — точку О и соединяют ее с точкой М , находящейся на контуре. Планиметр ставят острием в точку О и слегка нажимают на топорик, чтобы получить след на бумаге А . Затем иглой обводят занимаемую площадь, сначала по прямой ОМ до контура, далее делают полный оборот по контуру до точки М и, наконец, снова возвращаются в исходную точку О . После этого легким нажимом фиксируют на бумаге новое положение топорика В . Площадь, ограниченная контуром, равняется произведению длины планиметра АО на расстояние АВ между начальным и конечным положениями топорика: s = AO·АВ .

Для уточнения результата и исключения ошибки от несовпадения точки О с центром тяжести фигуры надо повернуть инструмент на 180° и сделать новый обвод в противоположном направлении. За окончательный результат принимают среднее из двух значений. Планиметр-топорик очень прост в работе и может с успехом применяться для измерения площадей с точностью, не превышающей 2–3 %.

На мелкомасштабных обзорных картах, которые содержат большие искажения, площади можно определять по клеткам картографической сетки. Размеры площадей клеток выбирают из таблиц, которые можно найти почти в каждом географическом атласе, например в атласе для учителей. Частично занятые клетки, так называемые до-мерки, оценивают на глаз с точностью до десятых долей. Для большей точности клетки картографической сетки делят на более мелкие с таким расчетом, чтобы их площади можно было найти в таблицах.

Мы знаем, что кратчайший путь между какими-либо двумя точками проходит по дуге большого круга, которая называется ортодромией. Ее можно построить с помощью глобуса. К намеченным на нем пунктам прикладывают нить, которая и соответствует ортодромии — дуге большого круга. Для переноса ее на карту определяют широты и долготы точек пересечения ортодромии с меридианами или параллелями. Запись координат можно вести в табличной форме. Дадим ее, например, для трассы Москва — Гавана.

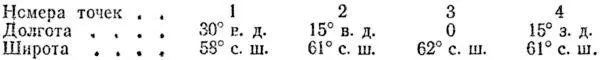
По данным координатам наносят на карту точки и затем соединяют их плавной кривой линией. Эта линия является трассой кратчайшего воздушного пути самолетов, следующих из Москвы в Гавану и обратно.

Такую задачу можно решить и без глобуса, по карте северного или южного полушария. Допустим, нам требуется узнать кратчайший путь между городами Махачкала и Владивосток, широта которых почти одинакова (рис. 40, а).

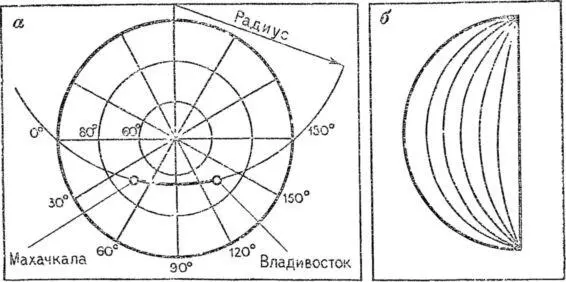
Рис. 40. Способ нахождения по карте полушария кратчайшего пути.

Возьмем циркуль и, передвигая его иглу вдоль линии меридиана, расположенного посередине между пунктами, подберем такой радиус, чтобы дуга окружности проходила через оба пункта и опиралась, на диаметр полушария. Кратчайший путь в нашем примере проходит по дуге, показанной на рисунке утолщенной линией. Данный прием нанесения кратчайшего маршрута на карту полушария можно применить и для пунктов, имеющих различную долготу и различную широту. Однако в последнем случае подобрать радиус и найти центр окружности, дуга которой проходила бы через оба пункта и концы диаметра, не так-то легко. Значительно проще подобные задачи решать с помощью палетки, изготовленной из прозрачного материала (кальки, целлофана). Делается она так. Лист кальки накладывают на карту полушария и переносят на нее с карты полуокружность. Затем через равные промежутки строят дуги, соединяющие концы полуокружности (рис. 40, 6).

Чтобы определить кратчайший путь между двумя пунктами, совместим линию полуокружности на палетке с линией окружности на карте. Поворачивая палетку вокруг центра полуокружности, добьемся такого положения, когда оба пункта окажутся на одной какой-либо дуге. По этой дуге и будет проходить кратчайший путь. Нужно только еще раз проверить точность совмещения линии на палетке с дугой окружности на карте.

Естественно, возникает вопрос: нет ли такой карты, на которой ортодромия изобразится в виде прямой? Есть такая карта. Она составлена картографами в азимутальной проекции, в которой проецирующие линии исходят из центра шара. В этом случае любое сечение шара, проходящее через центр, будет проектироваться на плоскость, касательную к поверхности шара, в виде прямой. Дело в том, что центр шара является одновременно центром любого сечения, делящего шар пополам, т. е. центром любого большого круга. При проецировании большого круга из центра шара мы получим безгранично расширяющуюся плоскость, которая, пересекаясь с плоскостью проекции, будет всегда давать прямую.

Ортодромия на карте показывает направление кратчайшего пути. Но по этому направлению масштаб будет отличаться от главного, который подписан на карте. Мало того, он будет разным в различных частях маршрута. Как же в таком случае определить расстояние по маршруту между начальным и конечным пунктами?