Алексей Куприн - Слово о карте

Оригинальный способ решения такой задачи предложил русский математик П. Л. Чебышев. Прежде всего находят географические координаты пунктов, между которыми определяют расстояние. Затем вычисляют разности координат, не учитывая знаков, и разность широт умножают на 120, а разность долгот — на 60. Большее из полученных двух чисел умножают на 7, а меньшее — на 3. Складывают оба числа, сумму делят на 7,5, и в результате получают расстояние между пунктами в километрах.

В качестве примера определим расстояние между Москвой и Ленинградом по их координатам.

Москва: 55,7° с. ш., 37,5° в. д.;

Ленинград: 59,9° с. ш., 30,3° в. д.

55,7°-59,9° = 4,2·120 = 504·7 = 3528;

37,5°-30,3° = 7,2·60 = 432·3 = 1296.

Сумма полученных чисел равна 4824. При делении этого числа на 7,5 получим расстояние между Москвой и Ленинградом, равное 643 км.

Данный способ приближенный. Более точные результаты можно получить по номограмме (рис. 41).

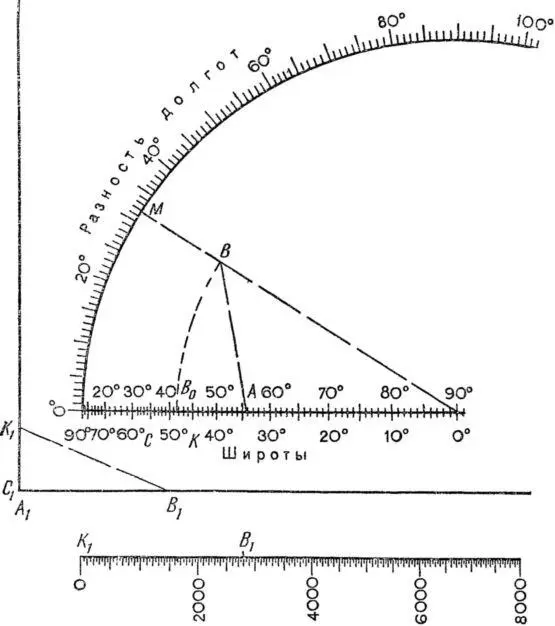
Рис. 41. График для определения расстояний между пунктами .

Порядок работы с помощью номограммы рассмотрим на следующем примере.

Определить расстояние между Москвой и Ташкентом по их координатам (Ташкент: 41,3° с. ш., 69,3° в. д.).

1. На круговой шкале отметим разность долгот пунктов 31,8° и соединим полученную точку М с центром круговой шкалы.

2. На верхней горизонтальной широтной шкале отложим точки А и В 0 , соответствующие широтам пунктов, и проведем из центра О дугу радиусом ОВ 0 . При пересечении с линией ОМ отметим точку В и соединим ее с точкой А .

3. На нижней широтной шкале отметим точки С и К , также соответствующие широтам пунктов.

4. На сторонах прямого угла отложим отрезки С 1К 1 и А 1В 1 ,равные соответственно СК и АВ . Отрезок К 1В 1 является гипотенузой прямоугольного треугольника.

5. Отложим отрезок К 1В 1 на самой нижней шкале и получим ответ: расстояние между пунктами равно 2800 км.

При тщательной работе с циркулем-измерителем расстояния с помощью увеличенной номограммы можно определять с точностью до 10 км.

Из всех географических карт топографические карты — самые точные и подробные. По ним можно определить, например, не только точные географические координаты различных пунктов, но и прямоугольные. Для удобства пользования прямоугольными координатами на каждом листе топографической карты имеется сетка квадратов, которую называют километровой. Она образована взаимно перпендикулярными линиями, проведенными через 2, 4 или 10 см. У всех линий километровой сетки даны подписи координат, которые необходимы не только для нанесения пунктов по заданным координатам, но и для отыскания объектов на карте. Для этого вначале указывают число, подписанное у нижней горизонтальной стороны квадрата, в котором расположен пункт, а затем у левой вертикальной.

Действительную наглядную картину местности создают на топографической карте с помощью условных знаков. Без знания условных знаков невозможно прочитать карту, также, как нельзя прочитать книгу, не зная букв. Условные знаки, принятые для наших топографических карт, просты, удобны для запоминания и в большинстве своем имеют начертание, напоминающее внешний вид изображаемого предмета местности.

К изобразительным свойствам условных знаков, кроме внешнего подобия, относится и цвет. Он придает карте красочность, наглядность, позволяет обогатить ее содержание. Цвета, принятые для некоторых условных знаков, соответствуют окраске изображаемых объектов. Так, лесные массивы, кустарники, сады и парки изображают зеленым цветом; моря, реки, озера, источники — голубым; элементы рельефа — коричневым. Это — традиционные цвета, применяемые на картах всего мира. Другие цвета имеют меньшее распространение.

В своем начертании условные знаки имеют такие элементы, которые позволяют определять точное местоположение любого объекта. Ими являются точки и линии контуров, осевые линии дорог и главные точки внемасштабных условных знаков, находящиеся в строго определенных местах значков в зависимости от их формы (в центре знака, середине основания или вершине угла).

Обратите внимание: условные знаки отдельного дерева, ветряного двигателя, бензоколонки и некоторых других предметов имеют у основания подсечку в виде черточки, направленной вправо. Эта подсечка имеет давнюю историю. Когда-то для наглядности карты условные знаки оттенялись. Оттенение их производилось в определенном порядке, принимая во внимание условное освещение местности с северо-запада на юго-восток. На топографических картах север находится наверху, а запад слева, поэтому изображаемые местные предметы предполагались освещенными сверху и слева. При таком условном освещении стороны предметов, находящихся в тени, изображались утолщением их очертаний. У возвышенных предметов оттенялись правые и нижние стороны. Углубленные предметы, такие, как реки, пруды, озера, оттенялись утолщением их левых и верхних берегов.

А как же оттенять внемасштабные условные знаки, у которых имеется всего одна вертикальная линия? Вот для них в то время и условились давать у основания небольшую подсечку вправо, которая изображает как бы тень от предмета.

Основу содержания топографических карт составляют графические условные знаки. В дополнение к ним для качественной характеристики предметов местности применяют буквенно-цифровые обозначения. Они дают возможность более объективно оценить тот или иной объект местности. Вот, например, что можно узнать о реке по буквенно-цифровым обозначениям: ширину, глубину и скорость течения реки, характер грунта дна, глубину бродов, размеры и грузоподъемность мостов, паромов.

По буквенно-цифровым обозначениям можно решать различные практические задачи. Например, пусть на территории области протекают две реки: Шуя и Сан (рис. 42).

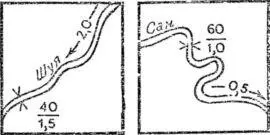
Рис. 42. Какая река более полноводна?

Какая из рек более полноводна и на какой можно построить более мощную гидроэлектростанцию?

Для решения задачи нужно прежде всего знать среднюю скорость течения воды в каждой реке. Топографы очень предусмотрительны, и, зная, что скорость может потребоваться для разных расчетов, они определяют ее во время съемки. Скорость течения выражают числом метров, преодолеваемых рекой за одну секунду, и подписывают на карте в разрыве стрелки, указывающей направление течения. Нужно знать еще поперечное сечение водного потока — то, что называют площадью живого сечения реки. Для определения этой величины воспользуемся другими числовыми данными — шириной и глубиной реки. Их подписывают на карте в виде дроби, в числителе которой указана ширина, а в знаменателе — глубина реки в метрах. Все необходимые данные у нас имеются.