Алексей Куприн - Слово о карте

По карте измеряют не только протяженность маршрута, но и длину реки, береговой линии озера, моря и других линейных географических объектов. И если измерений много, то целесообразно изготовить специальную палетку (рис. 35).

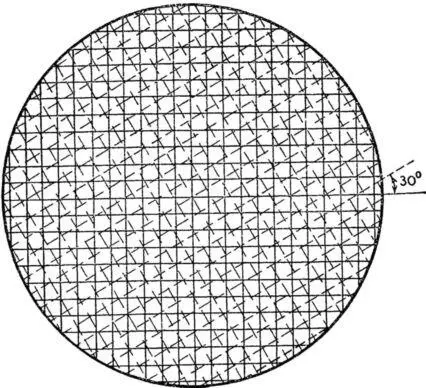
Рис. 35. Палетка для измерения расстояний по карте .

Ее делают из прозрачной основы, на которую наносят разным цветом две сетки квадратов, расположенные относительно друг друга под углом 30°. Каждая сторона квадрата сеток равна 3,82 мм. При определении длины линии палетку накладывают на карту так, чтобы концы измеряемой кривой оказались внутри сетки. Подсчитывают число сторон квадратов, пересекаемых измеряемой линией, вначале по сетке одного цвета, а затем, не сдвигая палетки, — по сетке другого цвета. Вычисляют среднее арифметическое из отсчетов по двум сеткам, и утроенное значение полученной величины даст длину измеряемой линии в миллиметрах.

Можно обойтись и одной сеткой, но в таком случае счет пересечений ее сторон с измеряемой линией придется вести при двух ее положениях. Вначале сетку располагают так, чтобы ее стороны были параллельны рамкам карты, а затем сетку поворачивают примерно на 30°. Если же отсчеты произвести при трех положениях сетки, т. е. после первого поворота, повернуть ее еще раз на 30°, то суммарное число пересечений даст искомую длину линии в миллиметрах.

Измерения расстояний производят по картам, на которых искажений нет или они практически незаметны. К ним относятся прежде всего топографические карты, а также карты районов, областей, краев, союзных республик, отдельных государств, протяженность которых с юга на север или с востока на запад не превышает 1500–2000 км. Но даже и на таких картах, как бы точно ни измеряли расстояния, они не будут соответствовать истинным. Это происходит потому, что в результате картографических обобщений извилистые линии на картах бывают укорочены по сравнению с реальными. На топографической карте, например, масштаба 1:200 000 несоответствие достигает 25 %.

Измерять расстояния на мелкомасштабных картах сложнее, чем на крупномасштабных, так как приходится считаться с переменным масштабом. Однако во многих случаях частные масштабы по всей карте или хотя бы на некоторых участках ее настолько мало отличаются от главного масштаба, что с достаточной для практики точностью масштаб считают постоянным. Наиболее точно длину по мелкомасштабной карте можно определить, если расстояние между точками измеряют по меридиану или по параллели. Определив разность широт или долгот начальной и конечной точек, умножают ее величину на длину дуги в 1° по меридиану или параллели и получают заданное расстояние. В качестве примера определим протяженность Каспийского моря с юга на север по меридиану 50°. Для этого определим по карте географические широты точек пересечения береговой линии моря с пятидесятиградусным меридианом. Они получились равными 46,5 и 37,5° с. ш. Разность их составляет 9°, что соответствует расстоянию 999 км (9·111).

Это расстояние (округленно 1000 км) соответствует длине Каспийского моря от устья Волги до берегов Ирана. Его можно использовать при изучении Европы и Азии в качестве сравнительного эталона для глазомерной оценки расстояний между различными пунктами. Подобные эталоны можно наметить и для других стран мира. Например, для Африки — длина Красного моря — 2000 км, для Северной Америки — длина полуострова Калифорния — 1200 км, для Австралии — длина мыса Йорк — 800 км.

На морских картах, которые строятся в проекции Меркатора, не дается линейный масштаб. Его роль выполняют восточная или западная стороны рамки карты, представляющие собой меридианы, разбитые на деления через 1' по широте. У моряков расстояния принято оценивать в милях. Морская миля — это средняя длина дуги меридиана в 1' по широте, равная 1852 м. Таким образом, рамки морской карты фактически разбиты на морские мили. Определив расстояние между двумя точками на карте в минутах меридиана, получают действительные расстояния в морских милях.

Если точки А и В расположены не на одном меридиане (рис. 36), то раствор циркуля-измерителя нужно перенести на рамку так, чтобы обе иглы циркуля отстояли на одинаковых расстояниях от концов проекций измеряемой линии.

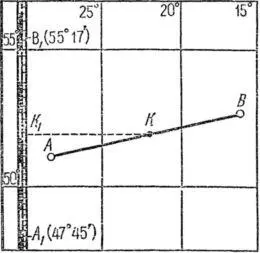
Рис. 36. Схема определения расстояний на морской карте.

Для этого вначале намечают в середине отрезка точку К и проектируют ее на боковую сторону рамки. От этой точки К 1 откладывают отрезки К 1А 1 и К 1В 1 ,равные отрезкам КА и КВ . Расстояние АВ в милях равно разности отсчетов широт точек А 1 и В 1 . В нашем случае оно получилось равным 452 милям (55°17′— 47°45′ = 7°32′ = 452').

Если предстоит длительная работа с мелкомасштабной картой, то имеет смысл изготовить специальный масштаб для измерения расстояний по разным параллелям. Образец такого масштаба приведен на рис. 37.

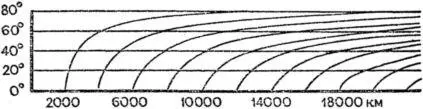
Рис. 37. Масштаб для измерения расстояний по разным параллелям .

Он представляет собой совокупность нескольких линейных масштабов, каждый из которых начерчен для соответствующего частного масштаба карты по различным параллелям. На нашем чертеже такие масштабы построены через 20° по широте. Нижняя горизонтальная линия соответствует масштабу на экваторе, следующая за нею — частному масштабу на параллели 20° и т. д. Отдельные точки масштаба соединяются плавными кривыми, что дает возможность измерять по масштабу длины линий, лежащих на промежуточных широтах.

Карта позволяет ответить и на такие вопросы, как, например, сколько гектаров занимает озеро, на какой площади раскинулся город и т. п. Наиболее просто и быстро площадь по карте можно определить графическим путем. На контуре, в пределах которого требуется определить площадь, на глаз строят равновеликий прямоугольник (рис. 38, а).

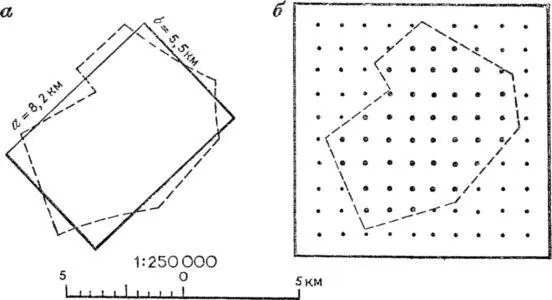
Рис. 38. Схема определения площади: а — построением равновеликого прямоугольника; б — точечной палеткой .

Измерив его основание а и высоту b и перемножив одно на другое, получим площадь фигуры. Для более точных определений фигуру разбивают на сеть прямоугольников, квадратов и треугольников. Площадь каждого из них вычисляют по известным правилам геометрии. Сумма площадей отдельных фигур даст общую площадь, заключенную в контуре.