Яков Перельман - Занимательная арифметика [Загадки и диковинки в мире чисел]

Так, число 1579 в двенадцатеричной системе изобразится следующим образом:

Ответ: "(10)(11)7", или KЛ7. Проверка: 10 х 144 + 11 х 12 + 7 = 1579.

Выразите:

1) Число 1926 в двенадцатеричной системе.

2) Число 273 в двадцатеричной системе.

Нетрудно сообразить, что в каждой системе высшая цифра, какая может понадобиться, равна основанию этой системы без единицы. Например, в десятичной системе высшая цифра 9, в шестеричной — 5, в троичной — 2, в пятнадцатеричной — 14 и т. д.

Клинописные цифры вавилонской шестидесятеричной системы. Для записи целых чисел вавилоняне пользовались всего двумя знаками — 1 и 10; 60 изображалось знаком единицы, но с большим интервалом от следующих цифр.

Самая простая система счисления, конечно, та, для которой требуется меньше всего цифр. В десятичной системе нужны десять цифр (считая и 0), в пятеричной— пять цифр, в троичной — три цифры (1, 2 и 0), в двоичной— только две цифры (1 и 0).

Существует ли и "единичная" система? Конечно, — это система, в которой единицы высшего разряда в один раз больше единицы низшего, то-есть равны ей; другими словами, "единичной" можно назвать такую систему, в которой единицы всех разрядов имеют одинаковое значение. Это самая примитивная "система"; ею пользовался первобытный человек, делая на дереве зарубки по числу сосчитываемых предметов. Но между нею и всеми другими системами счета есть громадная разница: она лишена главного преимущества нашей нумерации — так называемого поместного значения цифр . Действительно: в "единичной" системе знак, стоящий на третьем или пятом месте, имеет то же значение, что и стоящий на первом месте. Между тем даже в двоичной системе единица на третьем месте (справа) уже в 4 раза (2 х 2) больше, чем на первом, а на пятом — в 16 раз больше (2 х 2 х 2 х 2). Для изображения какого-нибудь числа по "единичной" системе нужно ровно столько же знаков, сколько было сосчитано предметов: чтобы записать сто предметов, нужно сто знаков, в двоичной же — только семь ("1100100"), а в пятеричной — всего три ("400").

Вот почему "единичную" систему едва ли можно назвать "системой"; по крайней мере, ее нельзя поставить рядом с остальными, так как она принципиально от них отличается, не давая никакой экономии в изображении чисел. Если же ее откинуть, то простейшей системой счисления нужно признать систему двоичную, в которой употребляются всего две цифры: 1 и 0. При помощи единицы и нуля можно изобразить все бесконечное множество чисел. На практике система эта мало удобна — получаются слишком длинные числа [20] Зато, как увидим далее, для такой системы до крайности упрощаются таблица сложения и таблица умножения. ; но теоретически она имеет все права считаться простейшей. Она обладает некоторыми любопытными особенностями, присущими только ей одной; особенностями этими, между прочим, можно воспользоваться для выполнения ряда эффектных математических фокусов, о которых мы скоро побеседуем подробно в главе "Фокусы без обмана".

К арифметическим действиям мы привыкли настолько, что выполняем их автоматически, почти не думая о том, что мы делаем. Но те же действия потребуют от нас немалого напряжения, если мы пожелаем применить их к числам, написанным не по десятичной системе. Попробуйте, например, выполнить сложение следующих двух чисел, написанных по пятеричной системе:

Складываем по разрядам, начиная с единиц, то-есть справа: 3 + 2 равно 5; но мы не можем записать 5, потому что такой цифры в пятеричной системе не существует: 5 есть уже единица высшего разряда. Значит, в сумме вовсе нет единиц; пишем 0, а 5, то-есть единицу следующего разряда, удерживаем в уме. Далее, 0 + 3 = 3, да еще единица, удержанная в уме, — всего 4 единицы второго разряда. В третьем разряде получаем 2 + 1 = 3. В четвертом 4 + 2 равно 6, то-есть 5 + 1; пишем 1, а 5, то-есть единицу высшего разряда, относим далее влево.

Искомая сумма = 11 340.

Предоставляем читателю проверить это сложение, предварительно переводя изображенные в кавычках числа в десятичную систему.

Точно так же выполняются и другие действия. Для упражнения приводим далее ряд примеров, число которых читатель, при желаний, может увеличить самостоятельно:

При выполнении этих действий мы сначала мысленно изображаем написанные числа в привычной нам десятичной системе, а получив результат, снова изображаем его в требуемой недесятичной системе. Но можно поступать и иначе: составить "таблицу сложения" и таблицу умножения" в тех же системах, в которых даны нам числа, и пользоваться ими непосредственно. Например, таблица сложения в пятеричной системе такова:

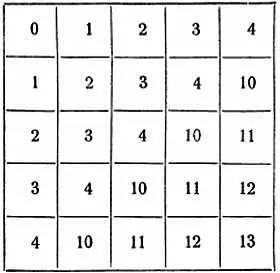
С помощью этой таблички мы могли бы сложить числа "4203" и "2132", написанные в пятеричной системе, гораздо менее напрягая внимание, чем при способе, примененном раньше.

Упрощается также выполнение вычитания.

Составим и таблицу умножения ("Пифагорову" [21] Пифагор (VI век до нашей эры) — древнегреческий философ; занимался также математикой и теорией музыки. ) для пятеричной системы:

Имея эту табличку перед глазами, вы опять-таки можете облегчить себе труд умножения (и деления) чисел в пятеричной системе, как легко убедиться, применив ее к приведенным выше примерам. Например, при умножении

рассуждаем так: трижды три "14" (из таблицы); 4 пишем, 1 — в уме. 1 на 3 дает 3, да еще 1, — пишем 4. Дважды три = "11"; 1 пишем, 1 переносим влево. Получаем в результате "1144".

Чем меньше основание системы, тем меньше и соответствующие таблицы сложения и умножения. Например, для троичной системы обе таблицы таковы:

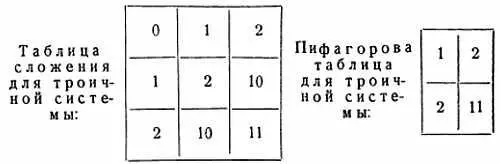
Их можно было бы сразу же запомнить и пользоваться ими для выполнения действия. Самые маленькие таблицы сложения и вычитания получаются для двоичной системы:

При помощи таких-то простых "таблиц® можно выполнять в двоичной системе все четыре действия . Умножения в этой системе, в сущности, как бы и вовсе нет: ведь умножить на единицу — значит оставить число без изменения; умножение же на "10", "100", "1000" (то-есть на 2, 4, на 8) сводится к простому приписыванию справа соответствующего числа нолей. Что же касается сложения, то для выполнения его нужно помнить только одно, что в двоичной системе 1 + 1 = 10. Не правда ли; мы с полным основанием назвали раньше двоичную систему самой простой из всех возможных? Длиннота чисел этой своеобразной арифметики искупается простотой выполнения над ними всех арифметических действий. Пусть требуется, например, умножить: