Лев Генденштейн - Алиса в стране математики

Но самое главное даже не в том, что Архимед смог назвать число, которое намного превосходит потребности даже современной науки. Главное в том, что он впервые ясно высказал идею о бесконечности натурального ряда — это, может быть, самая смелая «выдумка» за всю человеческую историю!

Поразив воображение древних греков, идея бесконечности стала с тех пор одной из главных во всей математике. Вот что пишут об этом самые крупные математики двадцатого столетия — немецкий учёный Гильберт и французский учёный Пуанкаре.

Гильберт: «Ни одна проблема не волновала так глубоко человеческую душу, как проблема бесконечности...»

Пуанкаре: «Если кто-нибудь захочет кратким и выразительным словом определить само существо математики, тот должен сказать, что математика — это наука о бесконечности».

Один древнегреческий учёный так выразил идею бесконечности: «где бы ни стал воин, он всегда сможет протянуть свое копье еще дальше »

Первыми начали изучать свойства натуральных чисел индийцы и греки — они заметили, что каждое натуральное число чем-то замечательно и не похоже на другие числа. Изменение всего-навсего на единицу меняет многие свойства числа — например, соседние числа никогда не делятся на одно и то же число. В древности были открыты и признаки делимости чисел (кстати, семь — единственное число из первого десятка, для которого нет удобного признака делимости — потому-то Шалтай-Болтай и похвалил Алису за расцвечивание натурального ряда всеми цветами радуги!).

То, что в воображаемом мире чисел существуют свои законы (например, сумма двух нечётных чисел — всегда чётное число!), навело учёных на мысль, что законы чисел могут быть связаны с закономерностями в окружающем мире . И действительно, древнегреческий учёный Пифагор, который жил в VI веке до нашей эры, открыл удивительную связь между законами чисел и законами музыки: например, если уменьшить длину струны или флейты вдвое , тон звука повышается точно на одну октаву . Это произвело на Пифагора такое впечатление, что он провозгласил: «число есть начало всех вещей».

Пифагор установил и первую связь между числами и фигурами: он ввел «треугольные» и «квадратные» числа.

Древние греки любили изображать числа камешками, раскладывая их на морском берегу. Так, например, они выкладывали «треугольные» числа. Как вы думаете, какие следующие «треугольные» числа?

Так выглядят «квадратные» числа. Мы и сейчас называем их «квадратами» — например, мы говорим: четыре в квадрате — шестнадцать. Какие следующие «квадратные» числа?

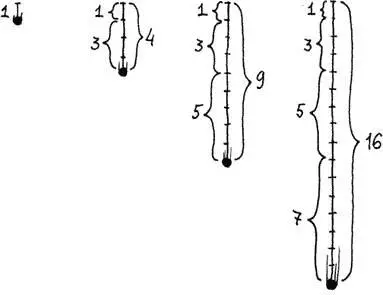
Пифагор обнаружил интересную связь между нечётными числами и «квадратными»: сумма последовательных нечётных чисел, начиная с единицы, обязательно будет «квадратным» числом! Например, 1 + 3 = 4, 1 + 3 + 5 = 9, 1 + 3 + 5 + 7 = 16 и так далее. На этом рисунке видно, как нечётное число, «пристраиваясь» к «квадратному», превращает его в следующее «квадратное» число

Прошло две тысячи лет после того, как Пифагор открыл связь между нечётными и «квадратными» числами, и это открытие помогло Галилею открыть один из важнейших законов природы. Когда Галилей изучал падение тел, он заметил, что путь, пройденный падающим телом за вторую секунду, втрое больше, чем за первую секунду, а путь, пройденный за третью секунду, в пять раз больше, чем за первую, и так далее. Отсюда Галилей сделал вывод, что путь прямо пропорционален квадрату времени движения — так и был открыт закон падения тел

Летя в межзвёздном пространстве, Алиса чувствовала себя как на мягкой-мягкой (бесконечно мягкой!) перине. Глаза её начинали слипаться, и она заснула.

Когда Алиса проснулась, всё вокруг изменилось до неузнаваемости: небо было уже не звёздным, а голубым, и на нем ярко сияло солнце. Купаться в солнечных лучах было очень приятно — оказалось, что Алиса порядком озябла в межзвёздном пространстве. Вдруг она вспомнила, что летит вслед за Шалтаем-Болтаем, повернула голову и увидела, что падает на город с островерхими башнями! Впереди неё падал Шалтай-Болтай — он всё так же медленно вращался и, кажется, спал.

Город был ещё далеко, и башни казались игрушечными, но они росли прямо на глазах. Алиса различила шпили на башнях и вся съёжилась. Однако скоро стало ясно, что они с Шалтаем-Болтаем падают на городскую площадь, посреди которой бьёт фонтан.

— Что же с нами будет? — в тревоге подумала Алиса, и в тот же миг Шалтай-Болтай упал на площадь и разбился. Скорлупа разлетелась на мелкие кусочки, но желток сохранился в целости.

— Если я упаду на него, то разобью его совсем! — мелькнуло в голове у Алисы.

Она закрыла глаза и изо всех сил пожелала, чтобы она не добила Шалтая-Болтая и не разбилась сама. В ту же секунду она всем телом ощутила упругую прохладу — ей показалось, что она упала на мокрый диван. Открыв глаза, Алиса обнаружила, что покачивается на вершине струи фонтана. Внизу, возле самого фонтана, в обломках скорлупы лежал Шалтай-Болтай.

Алиса соскользнула по струе и бросилась к Шалтаю-Болтаю. Желток всё ещё подрагивал после удара.

— Он жив! — обрадовалась Алиса. — Но как же его собрать?

Она огляделась: кусочки скорлупы были разбросаны по всей площади.

В этот момент на площадь выбежали два воина.

— Это, наверное, королевская рать, — догадалась Алиса. — Но неужели это вся рать? А где же конница?