Лев Генденштейн - Алиса в стране математики

Мы не случайно вспомнили о Санкт-Петербурге: в этом городе Эйлер провёл большую часть жизни, здесь же написал он и свою знаменитую работу о кёнигсбергских мостах. Работы Эйлера рождали порой новые области математики. Так произошло и с работой о кёнигсбергских мостах: с неё берёт начало топология — раздел математики, в котором изучаются самые общие свойства геометрических тел и фигур.

Что это за свойства? Представим себе, что у нас в руках кусок пластилина, и нам разрешается делать с ним, что угодно, но только не разрывать и не слеплять .

Пусть, например, кусок пластилина имеет сначала форму стакана. Мы можем превратить «стакан» в «ложку», нигде не разрывая и не слепляя пластилин:

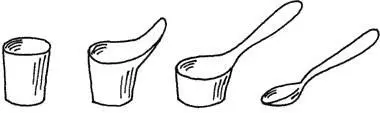
А вот превратить пластилиновый стакан в чашку с ручкой не удастся: ведь для ручки надо сделать дырку, то есть разорвать пластилин в каком-то месте, а мы условились, что разрывать и слеплять нельзя! Зато пластилиновую чашку можно превратить в бублик:

С точки зрения топологии стакан и ложка — это одно и то же, а чашка или бублик — совсем другое (однако чашка и бублик — тоже одно и то же!).

Далеко не всегда очевидно, что две фигуры «топологически одинаковы» — например, трудно поверить, что одну из этих пластилиновых «ручек» можно без разрывов и склеек превратить в другую, не снимая со стержня:

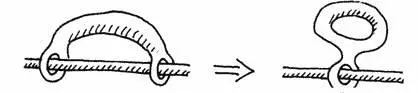
Однако вот промежуточные стадии такого превращения:

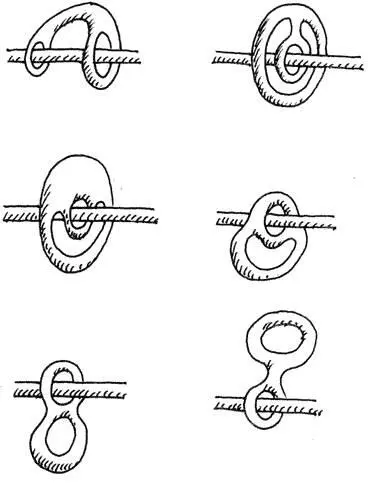
Задачи о кёнигсбергских мостах и о новом королевском за́мке — это настоящие топологические задачи: действительно, можно как угодно размещать башни и соединять их стенами любой формы, но пока мы не «разрываем» стен и не «склеиваем» их, задача остаётся той же самой!

Некоторые фигуры имеют настолько необычные топологические свойства, что перестаёшь верить собственным глазам. Одну из таких фигур обнаружил в середине XIX века немецкий учёный Мёбиус. Вы легко можете сами сделать «лист Мёбиуса» — возьмите полоску бумаги и склейте её в кольцо, повернув перед склеиванием на пол-оборота:

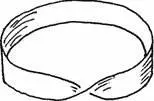
Чтобы убедиться в необычных свойствах листа Мёбиуса, попробуйте для начала покрасить его с одной стороны. Вы обнаружите, что карандаш или кисточка окрасят лист полностью ! Но так и должно быть — дело в том, что у листа Мёбиуса, в отличие от «обычных» поверхностей (то есть таких, к которым мы привыкли), не две стороны, а только одна !

А теперь попробуйте угадать, что получится, если разрезать лист Мёбиуса вдоль кольца посередине. Распадется ли он, например, на два кольца? Берите ножницы и режьте! Интересно, поверите ли вы своим глазам?

— А где же зал суда? — спросила Алиса: она читала в книжках, что суд происходит всегда в «зале суда».

— Залом будет этот двор, — показала Королева на один из трёх дворов за́мка.

Гости стали садиться прямо на траву, а для Короля и Королевы вынесли трон. Возле трона сразу же столпились какие-то карты и зверушки.

— Это, наверное, приближённые к трону , — догадалась Алиса (она не раз слышала о «приближённых к трону», но только теперь увидела, кто это такие!).

Сев на траву, Алиса обнаружила, что рядом с ней сидит Грифон.

— А где же Черепаха Будто? — спросила Алиса.

— Ползёт потихоньку прямо на бал, — ответил Грифон.

В этот момент Белый Кролик (он тоже оказался среди «приближённых к трону») поднял трубу и трижды протрубил.

Все замолчали, и в наступившей тишине Король Червей приказал Кролику:

— Читай обвинение!

Кролик развернул большой свиток пергамента и прочитал:

— Обвиняется Шляпник.

— А где обвиняемый? — поинтересовался Король.

— Его почему-то нет, — робко ответил Белый Кролик.

— Я есть! — раздался откуда-то голос Шляпника. Алиса обернулась и увидела, что Шляпник протискивается к трону между сидящими на траве.

— Почему ты опоздал? — строго спросил Король.

— Мартовский Заяц пригласил нас с Соней на чай... — начал Шляпник.

— Как! — вскричала Королева. — Из-за какого-то чая ты посмел опоздать на суд?

— Дело не в чае, а в часах, — сказал Шляпник. — Когда я пошёл к Мартовскому Зайцу, я забыл свои часы дома...

— Но разве у Зайца нет часов? — удивилась Королева.

— Часы у него, конечно, есть, — ответил Шляпник. — Но они остановились.

— Ну и что? — спокойно спросил Король. — Я уверен, что стоящие часы показывают точное время намного чаще, чем твои!

— И вовсе нет! — обиделся Шляпник. — С тех пор, как Заяц перестал смазывать мои часы сливочным маслом, они стали идти очень точно!

— Как точно? — поинтересовался Король.

— Они отстают всего на одну секунду в сутки, — похвастал Шляпник.

— На одну секунду в сутки? — переспросил Король. — Значит, за месяц они отстанут на полминуты?

— Всего-навсего! — радостно подтвердил Шляпник. — Я их не подвожу уже два месяца, и за это время часы отстали только на одну минуту!

— В часе шестьдесят минут, — сказал Король. — Значит, твои часы отстанут на час за сто двадцать месяцев...

— Это целых десять лет! — воскликнул Шляпник.

— А за сто двадцать лет твои часы отстанут на двенадцать часов, — продолжал Король.

— До этого, наверное, я уже не доживу, — вздохнул Шляпник.

— Зато тот, кто доживёт, наконец-то увидит на твоих часах точное время! — заметил Король.

— Почему? — удивился Шляпник.

— Только тогда, когда твои часы отстанут на двенадцать часов, их стрелки снова покажут точное время, — объяснил Король. — Разве не так?

— Так, — подтвердил озадаченный Шляпник.

— Вот и получается, что твои часы показывают точное время только один раз в сто двадцать лет ! — воскликнул Король. — А часы, которые стоят, показывают точное время два раза в сутки — это примерно в восемьдесят семь тысяч шестьсот раз чаще, чем твои! Так что, как видишь, твои отстающие часы намного хуже, чем часы Зайца, которые вообще стоят!