Лев Генденштейн - Алиса в стране математики

Бо́льшая часть знаний, которыми обладает человечество, получены с помощью умозаключений — ведь и то, что люди узнали опытным путем, они тоже должны были осмыслить

Но откуда берётся уверенность, что рассуждение правильно? Всегда ли можно доверять новому знанию, полученному посредством умозаключений?

Размышляя над этими вопросами, древнегреческий учёный Аристотель открыл законы мышления — правила, пользуясь которыми можно делать правильные умозаключения. Наука о законах мышления называется логикой от греческого слова «логос», что означает «мысль». Логикой Аристотеля мы пользуемся до сих пор.

Науку о мышлении Аристотель создавал не на пустом месте — у него были великие предшественники. С некоторыми из них мы уже знакомы. Так, Фалес, первый математик в истории, высказал идею доказательства , а доказательство — это как раз и есть установление правильности рассуждения. Строгих доказательств от своих учеников требовал и учитель Аристотеля Платон, который, в свою очередь, был учеником Сократа. Сократ учил рассуждать не только в математике, но и в жизни, причем учил очень интересным методом: он задавал вопросы, которые будили мысль у его собеседника — этот замечательный метод так и называется «сократовским». Сам Сократ был настолько мудр, что учился у каждого, кто мог сообщить ему что-то для него новое.

Особенность математики состоит в том, что правильность новых знаний можно установить только с помощью рассуждений — их невозможно проверить на опыте!

Объясним это на примере. Возьмём линейку, начертим на бумаге несколько разных треугольников и вырежем их. А затем обрежем у них углы — вот так:

Приложим теперь эти углы друг к другу. Мы обнаружим, что у всех наших треугольников сумма углов одна и та же — она равна как раз развёрнутому углу:

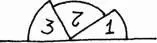
Мы получили новое знание: «у некоторых треугольников сумма углов равна развернутому углу». Это знание получено опытным путём. Но поскольку мы брали разные треугольники, у нас возникает догадка: может быть, у всех треугольников сумма углов равна развёрнутому углу?

Мы испытываем нашу догадку на десяти, ста, тысяче треугольниках и с радостью обнаруживаем, что она подтверждается! Однако можно ли считать, что мы её доказали ? Нет, нельзя — ведь в нашей догадке речь идёт о всех треугольниках, а их бесконечно много ! Там же, где появляется бесконечность, опыт бессилен (это слова французского математика Пуанкаре).

Поэтому здесь требуется математическое доказательство: можно доказать, что сумма углов у всех треугольников равна развёрнутому углу, если ... Вот это «если» и есть самое главное!

На что должно опираться математическое доказательство? Прежде всего, конечно, на уже доказанные утверждения (как мы помним, они называются «теоремами») . Но, оказывается, при этом возникает новая бесконечность, очень похожая на бесконечную цепочку вопросов «почему?» в беседе с четырёхлетним homo sapiens: вы отвечаете малышу на первый вопрос, но ваш ответ сразу же рождает у него второе «почему?», и ... новый ответ будет рождать новый вопрос без конца!

Учёные по своей любознательности почти не уступают четырёхлетним малышам, и поэтому они тоже столкнулись с бесконечной цепочкой вопросов и ответов — было это ещё в Древней Греции. И тогда стало ясно, что для того, чтобы можно было что-то доказать, какие-то утверждения придётся принять без доказательств , например: «через две точки проходит одна и только одна прямая». Такие утверждения греки назвали аксиомами , что в переводе с греческого означает «достойные почестей».

Главное требование к аксиомам состоит в том, чтобы они не противоречили друг другу (иначе получится так, как с «королевскими законами», которые придумывала Королева Червей). Непротиворечивость аксиом далеко не всегда очевидна: даже очень «правдоподобные» аксиомы могут противоречить друг другу! Вот известный шуточный пример. Возьмём три «аксиомы»:

1. Чем больше учишь, тем больше знаешь.

2. Чем больше знаешь, тем больше забываешь.

3. Чем больше забываешь, тем меньше знаешь.

Каждая из этих «аксиом» по отдельности не вызывает сомнений. Однако из трёх «аксиом» вместе следует вывод: «Чем больше учишь, тем меньше знаешь»! С этим странным выводом можно было бы и согласиться, но он противоречит первой «аксиоме»! А из второй и третьей «аксиом» следует вывод, который вообще противоречит сам себе: «Чем больше знаешь, тем меньше знаешь»! Так что волей-неволей приходится признать, что эти правдоподобные «аксиомы» противоречат друг другу.

Но даже непротиворечивых аксиом для доказательств теорем недостаточно. Надо ещё, чтобы тот, кто доказывает, и тот, кто его слушает, правильно понимали друг друга — ведь недоразумение может возникнуть просто из-за того, что они по-разному понимают значение одного и того же слова (помните спор Шляпника с Королевой о том, что такое «шляпа»?). Чтобы таких недоразумений не возникало, математики пользуются определениями . Если теорема отвечает на вопрос «почему?», то определение отвечает на вопрос «что такое?». Например:

— Что такое квадрат?

— Это прямоугольник, у которого все стороны равны.

Однако тут сразу же возникает новый вопрос:

— А что такое прямоугольник?

И уже можно догадаться, что нас снова подстерегает бесконечность, только на этот раз не вопросов «почему?», а вопросов «что такое?» . Поэтому некоторые понятия математикам пришлось принять за основные , то есть отказаться от попыток определить их. Например, основными понятиями являются «точка» и «прямая».

Когда есть основные понятия, аксиомы и правила логики, можно, наконец, доказывать теоремы! Теоремы — это и есть новые знания математиков: доказательством теорем математики занимаются со времён Фалеса до наших дней.

Через две тысячи лет после Аристотеля немецкий учёный Лейбниц задался целью создать универсальный язык науки, с помощью которого можно было бы записывать любые рассуждения в виде математических формул.