Мордехай Тульчинский - Качественные задачи по физике в средней школе и не только…

Увидеть аналогичный процесс наглядно можно, если в стакан воды положить кристаллик марганцовки: со временем вода вокруг кристаллика окрасится в фиолетовый цвет, причем в более теплой воде это произойдет быстрее (но пить это, конечно, ни в коем случае не надо!).

5. Можно ли сделать из мухи слона?

Возможна ли такая мутация с биологической точки зрения – вопрос к биологам, а мы рассмотрим физическую сторону задачи.

Представим себе, что мы увеличили муху в 100 раз. Это означает, что в 100 раз увеличились длина, ширина и высота мухи. Значит, объем мушиного тела вырос в 100 × 100 × 100 = 1 000 000 раз, а вместе с объемом во столько же раз увеличилась и масса (мы ведь не можем «собрать» муху из «других» атомов – в нашем распоряжении только то, что есть в Периодической таблице элементов).

При этом прочность мушиного тела увеличилась всего в 10 000 раз. Чтобы понять, почему так происходит, мысленно представим себе более простую конструкцию – прямоугольный брусок, скажем из дерева, и такой же брусок, габариты которого больше в 100 раз. Попробуем сломать бруски посередине. Для этого нам нужно разорвать связи между молекулами в поперечном сечении каждого бруска. Поскольку и ширина, и толщина большого бруска в 100 раз больше ширины и толщины маленького, то площадь поперечного сечения увеличилась в 100 × 100 = 10 000 раз. Количество молекул на единицу площади сечения будет одним и тем же и в маленьком бруске, и в большом. Значит, в большом бруске нам нужно разорвать в 10 000 раз больше молекулярных связей – и нам понадобится в 10 000 раз бóльшая сила.

Итак, чтобы лапы увеличенной в 100 раз мухи могли выдержать ее увеличившийся вес, нам нужно изготовить их из гораздо более прочного материала либо начать дополнительно их утолщать – а это уже не будет «муха в масштабе 1:100».

6. Три гонца и один график

Это задача становится очень легкой, если для ее анализа воспользоваться графическим методом. Изобразим траектории всех трех гонцов на графике зависимости координаты от времени. Точки на оси ординат соответствуют столицам Тридевятого королевства и Тридесятого царства, а за начало отсчета времени выберем момент отъезда первого гонца.

Графики движения гонцов будут представлять собой отрезки наклонных прямых, причем более пологая кривая соответствует меньшей скорости (за то же самое время более медленный гонец преодолевает меньшее расстояние).

На первый взгляд может показаться, что графики будут выглядеть так, как на рис. 27, то есть каждый гонец доставит свое послание.

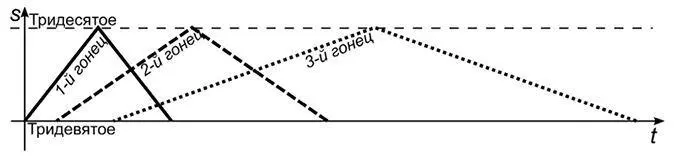
Рис. 27

Однако в условии задачи есть важный пункт: при встрече более медленный гонец отдает послание более быстрому. Это означает, что первый гонец на обратном пути встретит второго, заберет у него предложение о перемирии, отвезет царю и снова пустится в обратный путь. Второй гонец, отправившись назад, через какое-то время столкнется с третьим (пешим) гонцом, возьмет у него предложение руки и сердца, развернется и вновь выдвинется к Тридесятому царству, однако встретится с возвращающимся конным посланником, передаст документ ему, а сам поспешит домой. В конечном итоге все три послания в Тридесятое царство доставит первый гонец. Все эти перипетии отражены на рис. 28. (Могло ли получиться так, что первый гонец обгонит второго на обратном пути и сам заберет послание у третьего? Обоснуйте свой ответ.)

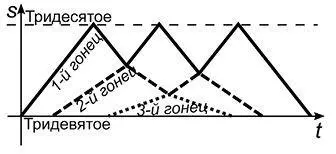
Рис. 28

Если бы в условии задачи были даны скорости гонцов, моменты их выезда и расстояние между столицами, после простых расчетов мы смогли бы по графику определить и время, за которое было доставлено каждое послание, и расстояние, которое преодолел каждый гонец, и время возвращения каждого из гонцов домой. Без графика эта задача решалась бы существенно сложнее. Попробуйте самостоятельно ответить на все эти вопросы, если скорости гонцов 40 км/ч, 20 км/ч и 10 км/ч, выехали они в 9.00, 13.00 и 18.00, а расстояние между столицами 200 км.

7. Сначала подумать, потом побежать

Если двигаться от точки A к точке B по прямой, получится самое короткое расстояние , но не самое короткое время . Здравый смысл подсказывает, что лучше немного больше пробежать по песку с большей скоростью, чтобы потом немного меньше проплыть по воде с меньшей скоростью. Может возникнуть искушение прибежать к той точке на берегу, которая находится прямо напротив тонущего человека, в этом случае длина заплыва будет самой маленькой, однако расчет показывает, что при этом спасатель слишком много времени потратит на бег. Тщательный расчет позволяет точно определить положение точки C на берегу, к которой нужно бежать и от которой нужно плыть. Сам этот расчет мы выполнить, к сожалению, не можем, потому что нужные для этого математические инструменты находятся за рамками школьной программы. А вот результат расчета будет вам вполне понятен, если вы уже знакомы с тригонометрией. Оказывается, спасатель должен выбрать такую промежуточную точку на кромке берега, чтобы отношение синусов углов, обозначенных на рис. 29, равнялось отношению скоростей спасателя на берегу и в воде:

sin α / sin β = v по песку/ v по воде.

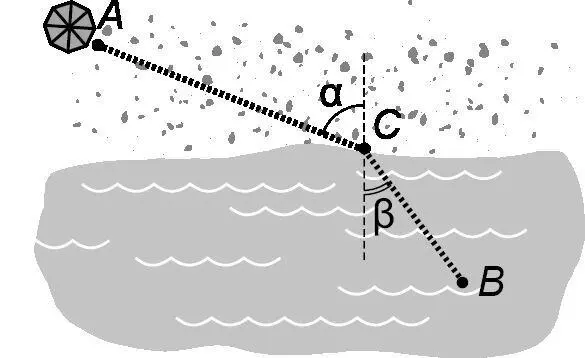
Рис. 29

Получающееся при этом правило математически повторяет закон Снеллиуса, описывающий то, как луч счета преломляется на границе двух сред с разной оптической плотностью. Дело в том, что свет ведет себя так же, как спасатель в этой задаче: он движется по тому пути, которое требует наименьшего времени . Это не обязательно самый короткий путь.

8. Мюнхгаузен на скачках

Обычный человек вообще не в силах передвигаться, неся лошадь на себе, но барон Мюнхгаузен, как хорошо известно, не был обычным человеком, так что такое разоблачение не вполне убедительно.

Чтобы вывести барона на чистую воду, отметим, что суммарное время, которое барон с лошадью затратили на два круга, не зависит от порядка кругов: не важно – сначала лошадь несла на себе барона, а потом барон лошадь или наоборот. Представим себе, что сначала барон нес на себе лошадь. Его скорость с лошадью на плечах была как минимум вдвое меньше скорости фаворита (15 верст в час против 30 верст в час). Это означает, что за то время, пока барон пробежал один круг, фаворит пробежал вдвое больше – то есть два круга – и закончил гонку. Чтобы хотя бы догнать фаворита, лошадь барона должна была бы пробежать второй круг мгновенно , не затратив вообще никакого времени. Сам барон, как существо сверхъестественное, возможно, способен и на мгновенные перемещения, но вот его лошадь – вряд ли.