Мордехай Тульчинский - Качественные задачи по физике в средней школе и не только…

(Заметьте: нам не понадобилось выяснять, что такое верста – достаточно было знать, что это единица длины.)

9. Рассеянный локомотив

На первый взгляд, в этой задаче недостаточно данных, и уж без расчетов в ней вроде бы никак не обойтись. Однако, если мы изобразим движение локомотива и вагона на графике зависимости скорости от времени (рис. 30), ответ получится практически сам собой.

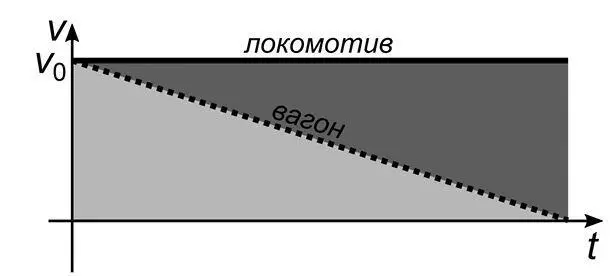
Рис. 30

За начало отсчета времени здесь взят момент въезда состава на мост. Поскольку, по условию, мост очень длинный, это позволяет пренебречь размерами – мы считаем и локомотив, и вагон материальными точками.

Чтобы сделать из этого графика вывод, нам нужно знать один простой факт: площадь под графиком зависимости величины скорости от времени численно равна пройденному пути. Для движения с постоянной скоростью это совершенно очевидно, потому что и пройденный путь, и площадь прямоугольника – это произведения скорости на промежуток времени (рис. 31).

Рис. 31

Для равнозамедленного движения это станет понятно, если заменить его движением со средней скоростью, которая равна среднему арифметическому начальной и конечной скоростей (рис. 32).

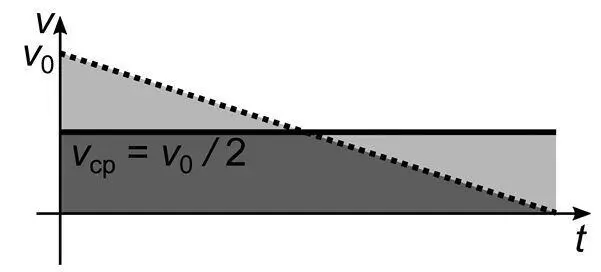
Рис. 32

Поскольку площадь прямоугольника на рис. 30 вдвое больше площади треугольника, это означает, что локомотив к моменту остановки вагона проехал вдвое больший путь, то есть доехал до второго конца моста.

10. Загадка железнодорожных колес

Если внимательно изучить железнодорожное колесо в профиль, можно заметить, что его диаметр у внешнего края меньше, чем у гребня (реборды), то есть колесо представляет собой не плоский цилиндр, а плоский усеченный конус. (В действительности форма колеса еще сложнее, да и рельс – не просто длинный металлический параллелепипед, но более глубокие нюансы нам придется отложить.) Когда колесная пара проходит поворот, она смещается наружу (вернее, рельс поворачивает из-под нее внутрь), и получается, что внешнее колесо катится по внешнему рельсу бóльшим диаметром, а внутреннее по внутреннему рельсу – меньшим.

11. Транспортировочная суета

Для начала разберемся в том, какое расстояние проходит помост от выкатывания одного бревна до выкатывания следующего. Из условий задачи (четыре бревна и помост длиной три метра) вытекает, что бревна располагаются в метре друг от друга. Значит, когда самое заднее бревно выкатилось, следующее находится в одном метре от заднего края помоста. Чтобы выкатиться, оно должно прокатиться по нижней части помоста один метр. Одновременно это бревно прокатится один метр по земле. Таким образом, помост сместится на два метра вперед. По условию задачи помост преодолел 100 метров, и каждые два метра из-под него выкатывалось следующее бревно – следовательно, Винкелю и Нуллиберу придется перенести заднее бревно вперед 50 раз.

После того как бревно выкатилось, до выкатывания следующего помост проходит 2 метра – и в этот момент приходит время подложить бревно впереди. Значит, выкатившееся бревно придется пронести (или прокатить) 2 метра вперед, а потом еще вдоль всего помоста – итого 5 метров. Умножая на 50 бревен, получаем, что за это время Винкель и Нуллибер пронесут или прокатят бревно на суммарное расстояние 250 метров (разумеется, это будут разные бревна – по очереди).

12. Кроличьи бега

Поначалу может показаться, что кролики будут просто гнаться друг за другом по кругу. Однако посмотрим внимательнее, куда направлена скорость отдельного кролика. Для этого возьмем центр шестиугольника O и соединим его с двумя соседними вершинами P 1 и P 2 (рис. 33). В самом начале скорость кролика, сидящего в вершине P 1, направлена к вершине P 2, потому что этот кролик начинает бежать прямо к своему соседу справа. Разложим эту скорость на две составляющие: составляющую вдоль отрезка OP 1 и перпендикулярную ей составляющую. Составляющая вдоль OP 1 отлична от нуля, а это значит, что кролик начнет смещаться в сторону центра O .

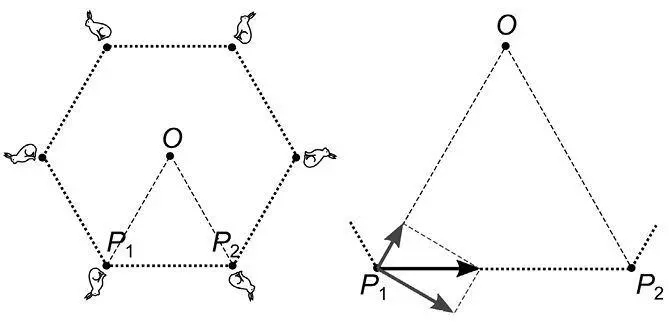
Рис. 33

Теперь воспользуемся принципом симметрии, который нередко помогает при решении физических задач. Симметрия и в физике, и в математике означает не только «зеркальное сходство» – смысл этого понятия намного шире. Систему называют симметричной, когда ее части в каком-либо смысле одинаковы или, другими словами, одна часть в каком-либо отношении ничем не лучше и не хуже другой. Одинаковые части должны вести себя одинаково – и это часто упрощает задачу.

В нашем случае ни один кролик не лучше другого, они все одинаковы, находились в одинаковых начальных условиях и продолжают вести себя одинаково. Значит, ни один из них не может находиться на другом расстоянии от соседа или от центра шестиугольника либо иметь другую по величине скорость по сравнению с остальными кроликами. Иначе говоря, кролики по-прежнему будут находиться в вершинах правильного шестиугольника с центром в точке O . Но, как мы выяснили раньше, каждый кролик при этом продвигается к центру шестиугольника – а значит, шестиугольник кроликов сжимается в размерах. Получается, что через какое-то время все кролики соберутся в точке O (и, вероятно, подерутся).

Если вы хорошо знакомы с тригонометрией, то сможете даже подсчитать, через какое именно время это произойдет, если сторона шестиугольника равна L метров, а скорость каждого кролика v м/с. (Подсказка: изящнее всего эта задача решается, если перейти в систему отсчета, которая вращается вокруг точки O таким образом, чтобы одна ее ось всегда смотрела на выбранного вами кролика. Угловая скорость вращения этой системы отсчета будет непостоянной, и при решении задачи на расчет сил такая система создала бы много проблем, но эту кинематическую задачу она существенно упростит.)

13. Шустрая грязь

Если мы перейдем в систему отсчета, связанную с велосипедом, а более точно – с его задней осью, которая движется так же, как и весь велосипед в целом, то увидим, что крайняя левая и крайняя правая точки колеса движутся в этой системе отсчета строго вертикально, крайняя нижняя точка движется назад, а крайняя верхняя – вперед (рис. 34).