Яков Перельман - Увлекательно о космосе. Межпланетные путешествия

Во сколько времени упал бы на Солнце земной шар, если бы от какой-нибудь причины прекратилось его движение по орбите?

Задачи подобного рода легко разрешаются на основании третьего закона Кеплера: квадраты времен обращения планет и комет относятся как кубы их средних расстояний от Солнца; среднее же расстояние от Солнца равно длине большой полуоси эллипса. В нашем случае мы можем земной шар, падающий прямо на Солнце, уподобить воображаемой комете, движущейся по сильно вытянутому эллипсу, крайние точки которого расположены: одна – близ земной орбиты, другая – в центре Солнца. Среднее расстояние такой кометы от Солнца, то есть большая полуось ее орбиты, очевидно, вдвое меньше среднего расстояния Земли. Вычислим, каков должен был бы быть период обращения этой воображаемой кометы. Составим на основании третьего закона Кеплера пропорцию:

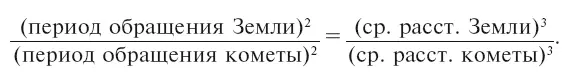
Период обращения Земли равен 365 суткам; среднее расстояние ее от Солнца примем за единицу, и тогда среднее расстояние кометы выразится через ½. Пропорция принимает вид:

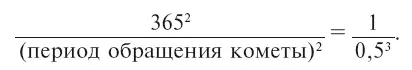
Откуда

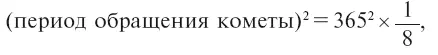
или

Но нас интересует не полный период обращения этой воображаемой кометы, а половина периода, то есть продолжительность полета в один конец – от земной орбиты до Солнца: это и есть искомая продолжительность падения Земли на Солнце. Она равна

Итак, чтобы узнать, за сколько времени Земля упала бы на Солнце, нужно продолжительность года разделить на √32, то есть на 5,6. Легко видеть, что полученное простое правило применимо не к одной только Земле, но и ко всякой другой планете и ко всякому спутнику. Иначе говоря, чтобы узнать, за сколько времени планета или спутник упадут на свое центральное светило, нужно период их обращения разделить на √32, то есть на 5,6. Меркурий, обращающийся за 88 дней, упал бы на Солнце за 15,5 дня; Сатурн, период обращения которого равняется 30 нашим годам, падал бы на Солнце в течение 5,5 года. А Луна упала бы на Землю за 27,3: 5,6, то есть за 4,8 сут. И не только Луна, но и всякое вообще тело, находящееся от нас на расстоянии Луны, падало бы к Земле в течение 4,8 сут. (если только ему не сообщена начальная скорость, а падает оно, подчиняясь лишь действию одного земного притяжения).

Здесь мы вплотную подходим к задаче Жюля Верна. Легко понять, что столько же времени должно лететь на Луну всякое тело, брошенное с Земли на Луну с такою скоростью, чтобы пройти как раз расстояние до Луны. Значит, алюминиевый снаряд Жюля Верна должен был бы лететь около 5 суток, если бы его хотели закинуть на расстояние Луны.

Однако члены Пушечного клуба рассчитывали закинуть снаряд не прямо на Луну, а только до той точки между Землей и Луной, где силы притяжения обоих светил уравниваются: отсюда снаряд сам уже упал бы на Луну, притягиваемый ею. Эта нейтральная точка находится на 0,9 расстояния от Земли.

Вычисление, следовательно, несколько усложняется. Во-первых, нужно вычислить, за сколько времени снаряд долетел бы до 0,9 расстояния между Землей и Луной или, что то же самое, за сколько времени тело с этого расстояния упало бы на Землю; во-вторых, надо определить продолжительность падения тела от этой нейтральной точки до Луны.

Для решения первой задачи представим себе, что на 0,9 расстояния от Земли до Луны обращается вокруг нашей планеты небесное тело, и вычислим период обращения этого воображаемого спутника Земли. Обозначив неизвестный период обращения через х, составляем на основании третьего Кеплерова закона пропорцию

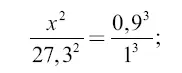
отсюда искомый период обращения .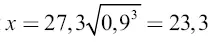

Разделив этот период на √32, то есть на 5,6, мы, согласно выведенному ранее правилу, получим время перелета снаряда от Земли до нейтральной точки: 23,3: 5,6 = 4,1 сут.

Вторую задачу решаем сходным образом. Чтобы вычислить, за сколько времени снаряд упал бы с расстояния нейтральной точки до Луны, нужно сначала определить, за сколько времени снаряд, находясь на том же расстоянии от Луны, совершил бы вокруг нее полный оборот. Радиус орбиты этого воображаемого спутника Луны равен 0,1 радиуса лунной орбиты, а масса центрального светила (в данном случае Луны) в 81 раз меньше массы Земли. Если бы масса Луны равнялась земной, то спутник, обращаясь на среднем расстоянии вдесятеро меньшем, чем лунное, совершил бы полный оборот в период у , легко вычисляемый по закону Кеплера:

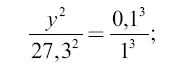
откуда

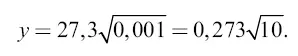
Но так как масса, а следовательно, и притягательное действие центрального светила в данном случае в 81 раз меньше, чем в системе Земли, то время обращения снаряда-спутника будет дольше. Во сколько раз? Из механики мы знаем, что центростремительное ускорение пропорционально квадрату скорости. Здесь это ускорение (производимое притяжением Луны) меньше в 81 раз, следовательно, скорость движения снаряда по орбите должна быть меньше в √81 раз, то есть в 9 раз. Другими словами, снаряд в роли лунного спутника должен обегать кругом Луны в 9 раз медленнее, чем он обходил бы на таком же расстоянии вокруг Земли. Значит, искомое время обращения равняется:

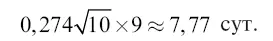
Чтобы получить продолжительность падения снаряда от нейтральной точки до Луны, нужно, как мы уже знаем, найденный сейчас период его обращения (7,77) разделить на √32, то есть на 5,6; получим 1,4 сут., а точнее – 33,5 ч. [46] На расстоянии Земли снаряд обращался бы вокруг Луны в 9 раз медленнее, чем Луна вокруг Земли, то есть совершал бы полный оборот в 27,3 × 9 сут. Время падения его с Земли на Луну под действием ее притяжения равнялось бы, следовательно, В такой срок должен был бы перелететь с Земли на Луну «кеворитный» снаряд Уэллса, если бы все его «кеворитные» заслонки были свернуты и вся масса снаряда подвергалась действию лунного притяжения. Но путешественники подвергали действию тяготения только часть массы снаряда, в движение же увлекалась вся масса снаряда. Вследствие этого снаряд получал ускорение, составляющее только некоторую долю нормального. В результате продолжительность перелета должна увеличиться. Если, например, действию притяжения подвергалась только 1 / 10 массы снаряда, то время падения снаряда на Луну должно возрасти в √10 раз, то есть путешествие длилось бы 136 дней.