Яков Перельман - Увлекательно о космосе. Межпланетные путешествия

Итак, весь перелет пушечного снаряда от Земли до Луны должен был бы длиться 4,1 + 1,4 сут. = 5,5 сут.

Однако это не вполне точный результат: здесь не принято во внимание то обстоятельство, что и при полете от Земли до нейтральной точки снаряд подвергается притягательному действию Луны, которое ускоряет его движение; с другой стороны, при падении на Луну он испытывает на себе замедляющее действие земного притяжения. Последнее действие должно быть особенно заметно и, как показывает более точное вычисление (по формуле, приведенной ниже), примерно вдвое увеличило бы продолжительность падения снаряда от нейтральной точки до Луны. Благодаря этим поправкам общая продолжительность перелета снаряда от Земли до Луны с 5,5 суток возрастает до 7 суток. В романе продолжительность перелета определена «астрономами Кэмбриджской обсерватории» в 97 ч. 13 мин. 20 с, то есть в 4 с небольшим суток вместо 7 суток. Жюль Верн ошибся на трое суток. Ошибка произошла от того, что романист (или лицо, производившее для него расчеты) преуменьшил время падения снаряда от нейтральной точки до Луны: оно определено всего в 13 ч. 53 мин., между тем как это падение должно было совершиться гораздо медленнее и отнять 67 ч.

Если тело падает без начальной скорости с весьма большого расстояния H не до центра притяжения, а до некоторого расстояния h , то продолжительность t (в секундах) такого падения вычисляется по следующей формуле, которая выводится в курсах интегрального исчисления:

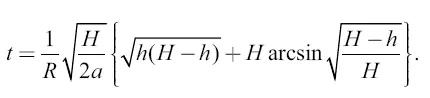
Здесь H и h имеют указанные выше значения, R – радиус планеты, а — ускорение тяжести на ее поверхности. По этой формуле вычисляется также продолжительность взлета тела от расстояния h до расстояния Н , где оно должно утратить всю свою скорость.

Для примера вычислим продолжительность взлета тела, брошенного с земной поверхности на высоту земного радиуса. В этом случае Н = 2R; h = R; а = g = 9,8; R = 6370.

Имеем продолжительность взлета:

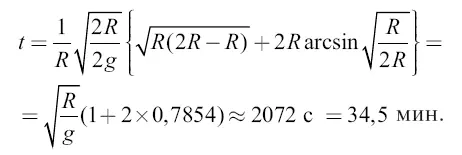
Значит, ракета, пущенная вверх на расстояние земного радиуса, должна возвратиться через 69 мин.

Для понимания дальнейшего необходимо отчетливо уяснить себе некоторые теоремы механики, относящиеся к количеству движения и к центру тяжести. Предпосылаем поэтому нашему изложению небольшую главу из «Курса физики» Гримзеля, где положения эти разъяснены весьма наглядно и с достаточной полнотой.

«Сила Р сообщает свободной массе m ускорение а , которое определяется из уравнения Р = ma. Если сила Р постоянна, то и ускорение постоянно, т. е. движение равномерно-ускоренное. Если постоянная сила Р действует на массу m в течение времени t, то она сообщает ей скорость υ = at. Чтобы оценить действие силы Р за время t , мы умножим выражение силы Р = ma на t. Мы получим равенство Р × t = m × υ .

Произведение Р × t называется импульсом силы Р за время t. Произведение т × υ называется количеством движения массы m , движущейся со скоростью υ . Импульс силы равен количеству движения массы, приведенной в движение этой силой.

Если действует сила переменная, то, строго говоря, этот закон можно прилагать лишь к малым промежуткам времени t, в течение которых силу можно считать неизменяющейся. Тогда предыдущее равенство принимает вид:

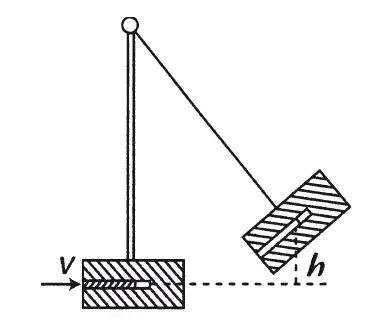
Рис. 57. Баллистический маятник

Понятия импульса и количества движения постоянно применяются в случаях, когда проявляются действие и противодействие.

Примером практического применения этих понятий может служить баллистический маятник, употребляемый для измерения скорости снаряда. Он состоит из большой, но податливой массы М (например, ящика с песком), которая подвешена на стержне, могущем вращаться около некоторой оси (рис. 57). В маятник стреляют снарядом, имеющим массу т , снаряд входит в песок и сообщает общей массе М + m некоторую скорость. Маятник отклоняется, и высоту его подъема Н измеряют. По высоте подъема вычисляют начальную скорость маятника 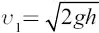. Количество движения, приобретенное маятником (вправо), есть Mυ 1; количество движения, приобретенное снарядом влево (или потерянное им, при счете вправо), равно:

mυ – mυ 1,

или

m ( υ – υ 1).

Итак,

Mυ 1 = т ( υ – υ 1),

или

mυ = ( М + m ) υ 1.

Отсюда можно вычислить υ.

В левой части последнего уравнения (mυ) стоит количество движения всей системы (маятник и снаряд) до выстрела, в правой части – количество движения системы после выстрела. Таким образом, количество движения системы не изменяется, если только в эту систему включены все взаимодействующие тела. Такая система называется замкнутой. Итак, в замкнутой системе количество движения остается неизменным, какие бы процессы внутри ее ни происходили. Это закон сохранения количества движения.

Другой пример представляет изображенный на рис. 58 двусторонний пистолет. На штативе горизонтально лежит медная трубка, на один конец которой навинчен массивный металлический цилиндр. Другой такой же цилиндр имеет насадку, плотно входящую в трубочку [47] Предполагается, что цилиндр с трубкой и цилиндр с насадкой имеют одинаковую массу. . В трубке сделано отверстие для поджигания с полочкой для пороха. Насыпав на полочку и в трубку немного пороха, вставляют снаряд и кладут пистолет на штатив. Затем при помощи раскаленной проволоки поджигают порох, насыпанный на полочку; порох в трубке взрывается – оба цилиндра с насадками получают ускорения в противоположные стороны и упадут на стол в одинаковых расстояниях от штатива. Действие взрыва одинаково в обе стороны и сообщает обоим цилиндрам одинаковые скорости.

Повторяют опыт с различными массами. Пусть цилиндр, скрепленный с трубочкой, весит 50 г, а вставляющийся в нее – 100 г. После взрыва первый отлетает вдвое дальше второго, хотя давление взрывных газов в обе стороны одинаково.

В каком бы отношении ни находились снаряды, всегда начальные скорости снарядов обратно пропорциональны их массам и, значит, произведения масс снарядов на начальные скорости одинаковы.