Яков Перельман - Увлекательно о космосе. Межпланетные путешествия

Читатели пожелают, вероятно, узнать, как вычисляется скорость, с которой тело должно покинуть планету, чтобы преодолеть силу ее притяжения. Вычисление основано на законе сохранения энергии. Тело должно получить при взлете запас кинетической энергии, равный той работе, которую ему предстоит совершить. Если масса тела т , а искомая скорость у, то кинетическая энергия («живая сила») тела в момент взлета

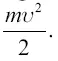
Работа же, совершаемая силой при перемещении с поверхности планеты в бесконечность (при отсутствии других центров притяжения), равна, как устанавливает небесная механика,

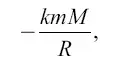
где М – масса планеты; R – ее радиус; а k – так называемая постоянная тяготения (см. Приложение 1). Абсолютную величину этой работы приравниваем к кинетической энергии:

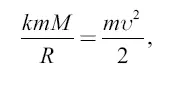
откуда

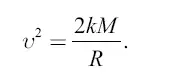
Далее, мы знаем, что вес тела на поверхности планеты, то есть сила, с какою планета его притягивает, равен, по закону тяготения:

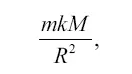
если масса тела m. Механика дает нам также и другое выражение для веса – произведение массы на ускорение, ma.

Значит,

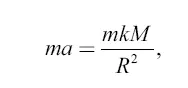
откуда

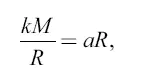
и, следовательно, формула

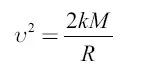
принимает вид:

υ 2=2 aR ,

откуда

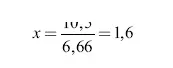
Подставляя вместо а ускорение тяжести на планете, а вместо R – радиус, получаем величину скорости, с какою тело навсегда покидает планету. Например, для Луны а = 1,62 м/с 2, R = 1 740 000 м. Поэтому искомая скорость

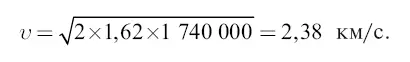
На том же можно основать вычисление начальной скорости снаряда или ракеты, которые, покинув Землю, должны долететь до точки равного притяжения между Землей и Луной. Масса Земли в 81 раз больше массы Луны, а так как сила притяжения уменьшается пропорционально квадрату удаления, то притяжения Земли и Луны уравниваются на расстоянии от Земли в 9 раз большем, чем от Луны (тогда притяжение Земли ослабеет в 9 × 9, то есть в 81 раз больше, чем притяжение Луны). Значит, точка равного притяжения лежит в 0,9 расстояния между Землей и Луной; последнее равно 60,3 радиуса R земного шара, так что ядро должно пролететь расстояние D = 0,9 × 60,3 R = 54,3 R . Обозначив искомую скорость, с какой тело должно покинуть Землю, через υ , имеем для кинетической энергии тела в момент вылета 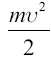, где m – масса тела. Произведенная же этим телом работа, по законам небесной механики, равна потерянной потенциальной энергии, то есть разности потенциальной энергии Е1 и Е в конечной и начальной точках пути. Поэтому

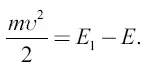
Здесь Е 1 есть потенциальная энергия тела в конечной точке пути по отношению к Земле и к Луне. Первая часть потенциальной энергии равна:

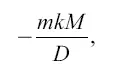
где k — постоянная тяготения; М — масса Земли; m – масса брошенного тела; D — расстояние тела от центра Земли в конечной точке пути.

Вторая доля равна потенциальной энергии (по отношению к Луне):

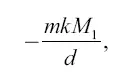
где k и m имеют прежние значения; М t– масса Луны; d – расстояние тела от центра Луны в конечной точке пути.

Величина Е есть потенциальная энергия тела (в точке земной поверхности) по отношению к Земле и Луне. Она равна

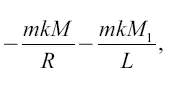
где R – радиус Земли; L – расстояние от поверхности Земли до центра Луны; а k, m, М и М 1имеют прежние значения. Итак,

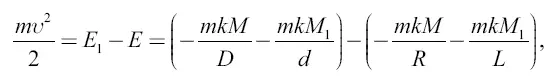
или

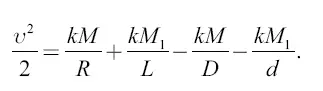
Подставим:

M 1= 0,012 M, D = 54,3 R ,

L = 59,3 R, d = 6 R .

Имеем:

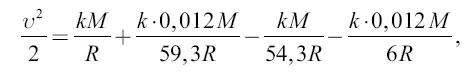
или

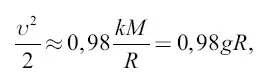
откуда

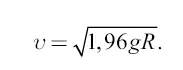
Известно, что

g = 9,8 м/с2;

R = 6370 км.

Выполнив вычисления, получаем искомую скорость

υ = 1 107 000 см/с = 11,07 км/с.

Указанным способом можно вычислить скорость и в других подобных случаях. Например, для определения скорости ракеты, взлетающей с Луны по направлению к Земле, имеем уравнение:

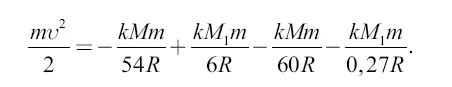
Здесь предполагается, конечно, что ракета должна достичь лишь точки равного притяжения, откуда начнется падение на Землю. Зная, что масса М 1 Луны равна 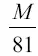, где М — масса Земли, имеем (после сокращения на m) :

откуда υ = 2,27 км/с – на 100 м меньше, чем скорость, вычисленная без принятия в расчет притяжения Земли. С такой же скоростью должно удариться о лунную почву тело, падающее на Луну из точки равного притяжения, имея Землю позади себя.