Яков Перельман - Увлекательно о космосе. Межпланетные путешествия

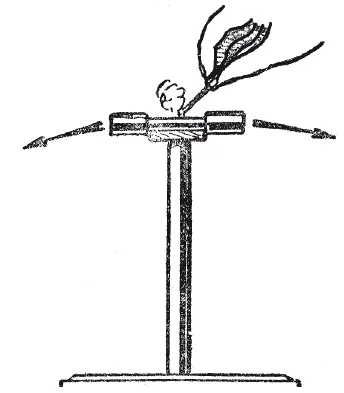
Рис. 58. Двусторонний пистолет

Движение снарядов можно определить таким правилом: если до взрыва весь пистолет был в равновесии относительно некоторой оси вращения, то это равновесие сохраняется в каждый момент после взрыва, причем путь обоих снарядов рассматривается как соединяющая их невесомая проволока, а вся система – как рычаг.

В самом деле, горизонтальные расстояния обоих снарядов от оси вращения в каждый момент движения обратно пропорциональны соответствующим массам, а это отвечает условию равновесия рычага. Воображаемая ось всегда проходит поэтому через центр тяжести обеих частей пистолета, так что положение центра тяжести остается неизменным (закон сохранения центра тяжести). Закон этот справедлив и для того случая, когда пистолет перед взрывом не был в покое, а двигался с постоянной скоростью. В этом случае после взрыва его части движутся так, что их общий центр тяжести продолжает свое прежнее движение с той же скоростью (сохранение движения центра тяжести). То же самое будет, конечно, при распаде на несколько частей – например, при движении осколков разорвавшейся гранаты или обломков распавшихся космических тел».

Рассмотрим теперь движение ракеты – сначала в среде, свободной от тяжести, а затем в условиях тяжести.

а) Движение ракеты в среде без тяжести. Ввиду фундаментального значения уравнения ракеты для всей теории звездоплавания приводим далее два ее вывода: один – элементарный, для незнакомых с высшей математикой, и другой – более строгий, с применением интегрального исчисления.

Пусть первоначальная масса покоящейся ракеты равна М t . Заменим непрерывное вытекание газа из трубы рядом последовательных толчков; с каждым толчком вытекает 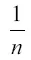массы M t ракеты со скоростью с . После первого толчка масса ракеты уменьшается до

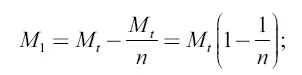
после второго толчка остающаяся масса ракеты равна

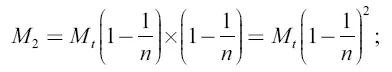
после третьего толчка

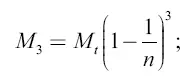
а после k-го —

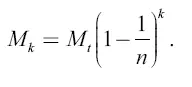
Скорость υ 1 , приобретаемую ракетой после первого толчка, легко вычислить, исходя из того, что общее количество движения всех частей ракеты до и после разъединения одинаково, то есть равно нулю:

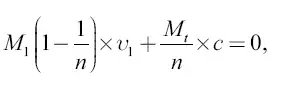
откуда

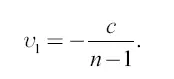
Скорость υ 2 после второго толчка можно считать равной 2 υ 1, то есть 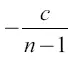, а после k-го толчка 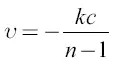, откуда

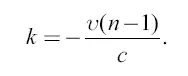
Подставив это выражение для k в формулу

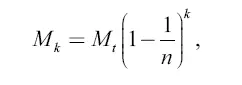
получаем

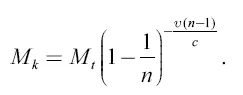
Преобразуем последнее выражение:

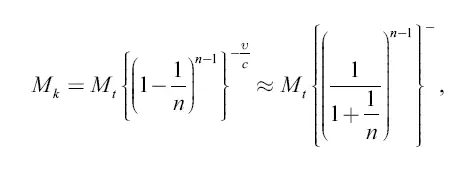
потому что

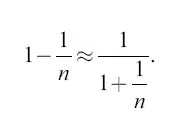
Выражение

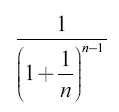
при бесконечно большом n (то есть при переходе от толчков к непрерывному вытеканию газа) равно, как известно, 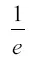, где е = 2,718. Тогда преобразуемое выражение получает вид:

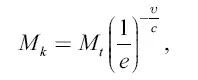
откуда получаем уравнение ракеты:

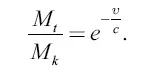
Укажем теперь более строгий вывод того же основного уравнения.

Обозначим массу ракеты в некоторый момент через М и предположим, что до горения ракета была неподвижна. Вследствие горения ракета отбрасывает бес конечно малую часть dM своей массы с постоянною скоростью с (по отношению к ракете). При этом остальная часть массы ракеты ( M— dM ) получает некоторую бесконечно малую прибавку скорости dυ. Сумма количества движения обеих частей ракеты должна быть, по законам механики (см. выше), та же, что и до горения, то есть равняться нулю:

cdM + ( M – dM ) dυ = 0,

или, по раскрытии скобок,

cdM + Mdυ – dMdυ = 0 .

Отбросив член dMdυ как бесконечно малую второго порядка (произведение двух бесконечно малых величин), имеем уравнение:

cdM + Mdυ = 0,

которое представляем в виде

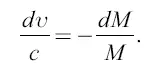
Интегрируя это дифференциальное уравнение, получаем:

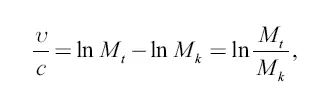
или

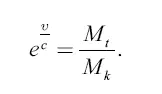
Мы пришли к уравнению ракеты, или ко второй теореме Циолковского, которую он формулирует так: «В среде без тяжести окончательная скорость (υ) ракеты не зависит от силы и порядка взрывания, а только от количества взрывчатого материала (по отношению к массе ракеты) и от устройства взрывной трубы».

При всех этих вычислениях не учитывалось земное притяжение, влияние которого мы сейчас вкратце рассмотрим.

б) Движение ракеты в условиях тяжести. Ускорение а , приобретаемое ракетой при отвесном подъеме с Земли, равно, очевидно, разности между собственным ускорением ракеты р и ускорением земной тяжести g :