Яков Перельман - Увлекательно о космосе. Межпланетные путешествия

Так производится расчет наличной скорости для артиллерийского снаряда, скорости, имеющей максимальное значение на земной поверхности. В случае ракеты скорость на уровне земной поверхности равна нулю и постепенно растет по мере взлета ракеты, пока не прекратится горение заряда. Следовательно, максимальную свою скорость ракета приобретает на некоторой высоте над Землей, где напряжение тяжести, естественно, меньше, чем на уровне моря. Поэтому максимальная скорость, уносящая ракету в межпланетный полет, меньше, чем для пушечного снаряда. Вычислим ее, сделав предпосылку, что ракета летит с ускорением, равным утроенному ускорению земной тяжести.

Обозначим высоту, на которой ракета приобретает максимальную скорость υ , через х. Известно, что υ 2= 2 × 3 g × x = 6 gx.

Потенциальная энергия единицы массы ракеты на уровне × равна, согласно предыдущему:

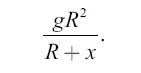
Потенциальная энергия той же единицы массы на высоте 54,37 R (в точке равного притяжения) выражается суммой

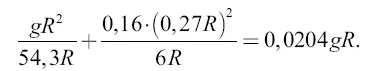
Потеря потенциальной энергии при перемещении ракеты с уровня x на уровень 54,37 R составляет

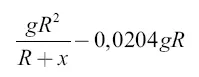
и должна, мы знаем, равняться кинетической энергии единицы массы ракеты, то есть 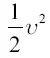, или 3gх. Имеем уравнение

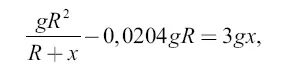
откуда x = 0,2616; R = 0,2616 × 6370 = 1666 км.

Теперь из уравнения υ 2= 6gх находим υ = 9750 м/с.

Итак, ракета, отвесно направляющаяся к Луне, достигает наибольшей своей скорости – 9¾ км/с – далеко за пределами земной атмосферы. Число секунд t , в течение которого накапливается эта скорость, определяется из уравнения 9750 = 3 × 9,8 t , откуда t = 321 с. Можно вычислить, что под действием земной тяжести ракета потеряет 321 × 7,76 = 2490 м своей секундной скорости (7,76 – средняя величина ускорения тяжести на протяжении 1666 км от земной поверхности). В общем итоге запас энергии, каким надо снабдить ракету для отвесного полета на Луну, должен отвечать скорости 9750 + 2490 = 12 240 м/с.

Сходным образом можно установить, что при отвесном подъеме ракеты с Луны она приобретает максимальную скорость (2300 м/с) на высоте 90 км после 76 с подъема. И обратно: падая от точки равного притяжения на лунную поверхность, ракета должна начать замедление полета на высоте 90 км, чтобы при ускорении (отрицательном) свести свою 2300-метровую скорость к нулю.

Вычисляя скорость, с какой тело должно покинуть Землю для удаления в бесконечность, мы принимали, что Земля – единственный центр, притяжение которого тело должно при этом преодолеть. На самом же деле приходится считаться также и с притяжением Солнца. Чтобы учесть это обстоятельство, установим сначала зависимость между скоростью тела на орбите и другими величинами.

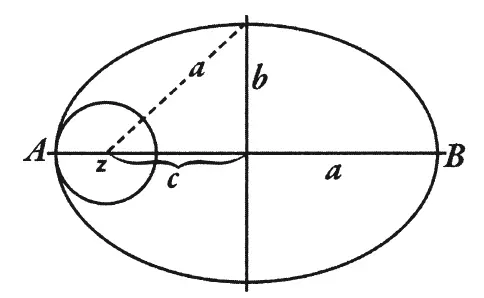
Рис. 59. К расчету скорости полета

По второму закону Кеплера площади, описываемые радиусом-вектором в равные времена, равны. Пусть тело (планета) движется вокруг Солнца по эллипсу с полуосями а и b ; период обращения Т секунд, секундная скорость υ , радиус-вектор r ; тогда для точек перигелия и афелия имеем равенство

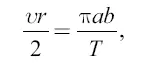
где левая часть есть выражение (приближенное) для площади, описываемой радиусом-вектором за 1 с, a π ab – площадь эллипса. Имеем:

Пусть теперь тело (звездолет, планета), движущееся вокруг Солнца по круговой орбите радиуса r , должно перейти в точке А своего пути на эллиптическую орбиту с полуосями а и b . Определим, какое для этого необходимо изменение скорости.

Из третьего закона Кеплера следует, что отношение квадрата периода обращения планеты к кубу ее среднего расстояния от Солнца (или большой полуоси) есть величина постоянная; для планет Солнечной системы эта постоянная равна (в единицах системы см – г – с)

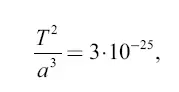
откуда

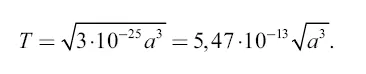
Отсюда имеем скорость у кругового движения около Солнца на расстоянии г.

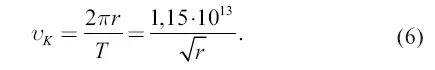
Обращаясь к эллиптической орбите, имеем прежде всего

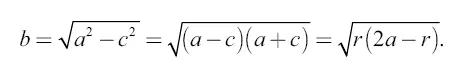
Из формулы (5) мы знаем, что скорость υ э движения по эллиптической орбите в точке А

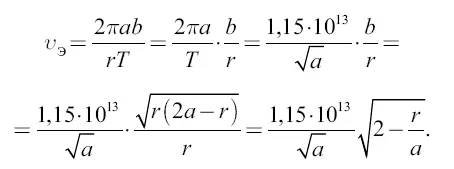
Так как скорость υ Kдвижения по круговой орбите (см. (6)

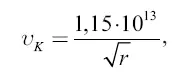
то из сопоставления формул (6) и (7) имеем

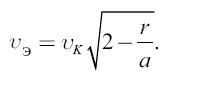
По этой формуле и вычисляется скорость, какую необходимо сообщить звездолету, чтобы с круговой орбиты он перешел на эллиптическую или удалился в бесконечность. В последнем случае полагаем большую полуось а эллипса равной бесконечности. Имеем

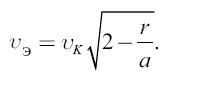
то есть для удаления звездолета с круговой орбиты в бесконечность необходимо, чтобы круговая скорость его увеличилась в √2 раз. Так, для удаления с земной орбиты (соответствующая скорость 29,6 км/с) в бесконечность нужна скорость

υ ∞ = 29,6√2 = 41,8,

то есть приращение скорости 41,8 – 29,6 = 12,2 км/с.

Теперь мы можем вычислить скорость, какая должна быть сообщена звездолету для преодоления притяжения Земли и Солнца и, следовательно, для свободного удаления с Земли в бесконечность. Чтобы преодолеть притяжение, нужна начальная скорость 11,2 км/с, то есть работа («живая сила») для каждого килограмма веса звездолета