Яков Перельман - Увлекательно о космосе. Межпланетные путешествия

a = p – g .

Так как приобретаемая при этом ракетой окончательная скорость υ 1= at 1, то продолжительность горения равна 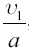, то есть

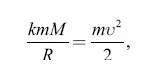
Из этого равенства и из соотношения υ = pt мы выводим, что при одинаковой продолжительности горения ( t = t 1):

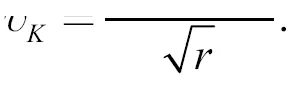
откуда

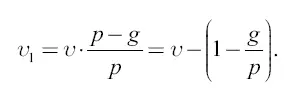
Значит,

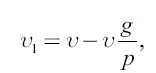
то есть окончательная скорость ракеты в среде тяжести меньше, чем в среде без тяжести, на такую же долю, какую ускорение ( g ) тяжести составляет от собственного ускорения ( р ) ракеты.

Далее, зная из предыдущего, что в среде без тяжести

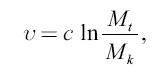
получаем, что окончательная скорость ракеты в условиях тяжести

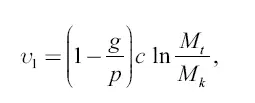
или

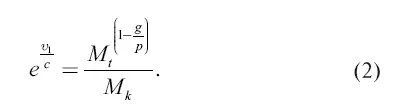
Формула (2) позволяет вычислить окончательную скорость, приобретаемую ракетой в поле тяготения, если известно отношение 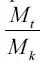масс заряженной и незаряженной ракеты и ее собственное ускорение р. Это последнее, мы знаем, не должно превышать четырехкратного ускорения земной тяжести, чтобы быть безвредным для человеческого организма. При р = 4g имеем

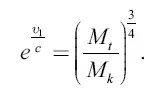
Формулы эти не принимают, конечно, в расчет сопротивление воздуха.

Подсчитаем, какую долю энергии потребляемого горючего ракета переводит в полезную механическую работу.

Обозначим, как прежде, массу свободной ракеты до взрывания через М t , после взрывания – через М k ; масса израсходованного горючего выразится тогда через M t—М k , скорость вытекания газа – с . Живая сила вытекающих газов, то есть кинетическая энергия, равна

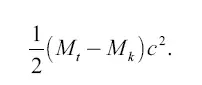
Отношение второй величины к первой и есть коэффициент к полезного действия свободной ракеты:

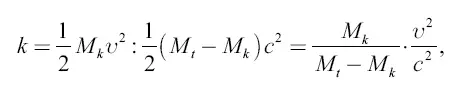
или

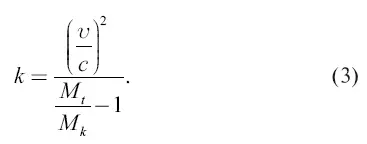
Из формулы (2) имеем, что

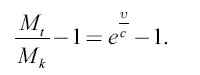
Значит, в среде без тяжести полезное действие ракеты:

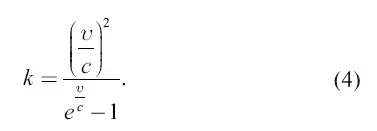
Оно достигает наибольшей величины при 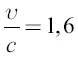и равно тогда 65 %.

Если 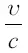невелико, можно формулу (4) упростить, исходя из того, что

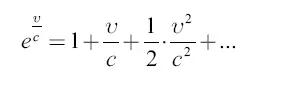
Тогда

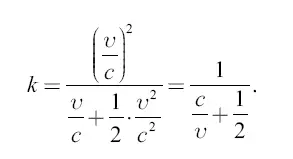
В среде тяжести выражение для к сложнее; для случая вертикального подъема его нетрудно вывести, подставив в формулу (3) соответствующее значение 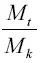из формулы (2).

Иначе выразится коэффициент к полезного действия ракетного экипажа (вообще несвободной ракеты), где существенную роль играют такие помехи движению, как трение и сопротивление воздуха. Рассмотрим случай равномерного движения авторакеты, то есть случай, когда работа ракеты равна работе сопротивлений. Так как импульс силы равен количеству движения, то, обозначая через / силу, выбрасывающую продукты взрыва (она равна силе, увлекающей автомобиль), а через t — продолжительность движения, имеем

ft = ( M t—M k ) c ,

где М t— масса автомобиля до взрывания; М к— его масса после взрывания; с — скорость вытекания газа. Для удобства обозначим М t– М к, то есть запас горючего, через Q , тогда

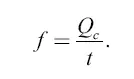
Полезная же работа автомобиля равна:

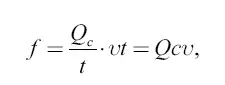
так как путь s = υt , где υ – скорость автомобиля.

Энергия, затраченная при этом, составляется из двух частей: 1) из той, которая была израсходована на приведение горючего в равномерное движение со скоростью υ ; эта часть равна 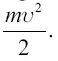; 2) из той, которая расходуется на сообщение частицам отбрасываемых газов скорости с; часть эта равна 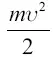. Вся затраченная энергия равна

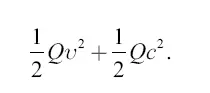
Отсюда искомое полезное действие

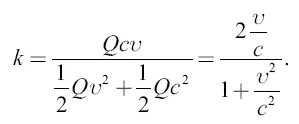
Оно достигает наибольшей величины при у = с, то есть когда автомобиль движется со скоростью вытекания продуктов взрыва.

По этой формуле легко вычислить полезное действие ракетного автомобиля; например, для с = 2000 м/с и у = 200 км/ч = 55 м/с:

k = 5,5 %.

Чтобы соперничать в экономичности с обыкновенным автомобилем, полезное действие которого около 20 %, авторакета должна обладать скоростью не ниже 760 км/ч. Но подобная скорость для колесного экипажа практически недопустима, так как сопряжена с опасностью разрыва бандажей колес центробежным эффектом.