Феофан Бублейников - О движении

Но вычисление площади круга, поверхности и объема цилиндра и шара было еще нерешенной проблемой для Евклида.

В «Началах» Евклида геометрия впервые была приведена в стройную систему. Это сочинение служит образцом строгости доказательств и последовательности изложения.

В течение более двух тысячелетий «Начала» служили руководством при изучении геометрии. Все великие математики прошлого начинали знакомство с геометрией по этой книге.

Евклид не стремился приложить свои математические способности к физике или технике. Он, правда, разработал учение об отражении лучей света от плоских и кривых зеркал. Но это было для него чисто геометрической задачей.

По свидетельству историков, о приложении геометрии к механике Евклид и не думал. Когда один юноша спросил его, какую пользу получит он от изучения геометрии, Евклид, по преданию, сказал своему слуге: «Дай этому человеку три обола [2] Обол — древняя греческая монета. Во времена Гомера оболом называли железный прут, который служил в качестве монеты. Поэтому позднее мелкую монету также назвали оболом. , он ищет от геометрии пользу».

Однако скоро нашелся ученый, который посмотрел на задачи механики с точки зрения геометрии.

До того времени механика была искусством техников, усваивавших различные чисто практические правила. Приложение к ней математики превратило механику в строгую науку.

Подобно геометрии, в механике делаются выводы, исходя из известных по опыту данных — аксиом.

Знаменитейший из древнегреческих математиков, Архимед (287–212 до н. э.) первый заложил основы современной механики.

Архимед был сыном знатного, но небогатого гражданина Сиракуз — астронома Фидия. Он получил образование в Александрии, где основательно познакомился с трудами Евклида и других математиков.

Математическим дарованием Архимед превосходил всех своих предшественников и современников. Он по праву признан одним из величайших геометров всех времен и народов.

Архимед за решением геометрической задачи.

Архимед первый вычислил с точностью до третьего десятичного знака отношение длины окружности к диаметру.

Он исследовал свойства эллипса, параболы и гиперболы — кривых, полученных сечением конуса плоскостью.

Математики знали, что если пересечь прямой конус плоскостью, наклонной к его высоте, то получится эллипс. Пересечение параллельно образующей дает параболу, а параллельно высоте — гиперболу.

Но каковы свойства этих кривых? Как вычислить площадь круга, эллипса или сегмента параболы и гиперболы? Архимед нашел путь к решению подобных задач, названный в средние века «методом исчерпывания». Этот метод он и применил для вычисления площадей фигур, ограниченных кривыми.

Как найти с помощью этого метода, например, площадь круга?

Архимед вписал в круг правильный шестиугольник. Площадь этой фигуры равна сумме площадей шести треугольников, на которые разобьется шестиугольник, если соединить его вершины с центром круга.

Площадь круга больше площади этого шестиугольника на сумму площадей шести сегментов, ограниченных его сторонами и дугами круга.

Удвоив число сторон шестиугольника, Архимед получил двенадцатиугольник, площадь которого ближе к площади круга.

Затем легко вписать двадцатичетырехугольник, еще более близкий к кругу. Так постепенно «исчерпывается» площадь круга.

Тот же метод Архимед применил для вычисления площади эллипса и сегмента параболы и гиперболы.

Геометрия была главным занятием Архимеда. Он отдавал этой науке большую часть своего времени и сил. Рассказывают, будто бы Архимед решал геометрические задачи даже сидя в ванне. Он чертил на песке у своих ног, на стенах домов, везде, где это было возможно.

Но в отличие от Евклида, Архимед очень интересовался не только механикой, но и техникой. Он изобретал различные машины. Им были придуманы механизм для подъема воды — архимедов винт, полиспаст и множество других машин.

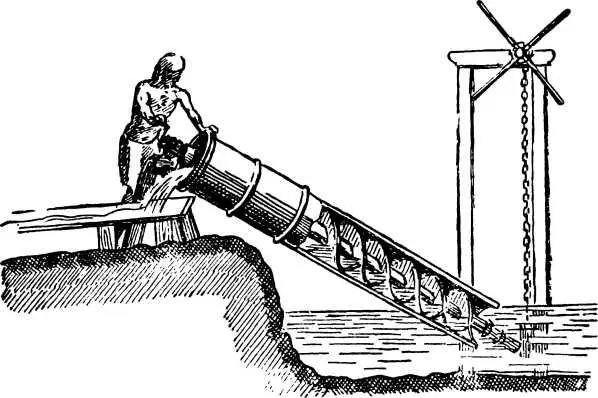
Архимедов винт — механизм для подъема воды.

Чтобы показать значение механического расчета, Архимед устроил ручную подъемную машину, при помощи которой он мог собственными руками передвигать и поднимать огромные тяжести. Рассказывали, будто бы он подтянул этой машиной к берегу большое трехмачтовое судно, нагруженное товарами и людьми.

Конечно, чтобы собственной силой сделать эту работу, Архимед должен был в течение очень долгого времени крутить рукоять бесконечного винта своей машины: ведь выиграть в силе можно, лишь потеряв столько же во времени. Присутствовавший при этом опыте царь Гиерон был поражен необычайным зрелищем. Но Архимед будто бы сказал ему: «Дай мне, где стать, и я сдвину Землю».

Как техник Архимед прославил свое имя при защите родного города, осажденного в 210 году до н. э. римлянами. Только благодаря техническому гению этого великого математика удалось в течение двух лет отбивать приступы закаленных в боях римских воинов.

О защите Сиракуз Архимедом Полибий, Плутарх и другие историки сохранили множество легендарных рассказов.

Машины Архимеда бросали в наступавших крупные и мелкие камни, тучи стрел и копий. Они поражали ряды воинов, разбивали деревянные прикрытия, не допускали к стенам города разрушительных таранов.

Еще более поразительны сильно преувеличенные рассказы о борьбе Архимеда с морскими судами римлян.

Со стен города на них сбрасывались тяжелые бревна. Спускавшиеся огромные когти захватывали суда, приподнимали их на воздух, а затем опускали в воду кормой или бросали их на скалы.

Римский корабль, опрокинутый машиной Архимеда.

«Придется нам прекратить войну против геометра, — сказал предводитель римлян Марцелл, — который поднимает вверх суда с моря и превосходит сказочного сторукого великана, бросая сразу на нас такое множество снарядов».

Римлянам удалось взять Сиракузы только вследствие недостаточной бдительности охраны города в одну из ночей. Архимед был, повидимому, случайно убит. На его могиле сограждане поставили невысокую гранитную колонну с выгравированным на ней рисунком шара, вписанного в цилиндр.

Через полтора столетия всеми забытая могила великого математика и защитника Сиракуз сровнялась с почвой. Стоявший на ней памятник был почти засыпан землей.