Лариса Вольницкая - Музыкальная геометрия мира: музыка и мы. Игра-эксперимент «Узел» в письмах к М.

Но кто такой Чжу Цзай-юй?

– Учёный, астроном, математик, лингвист и музыковед, изобретатель музыкальной темперации.

Так представляет его нам Энциклопедия.

Интернет может более обстоятельно познакомить тебя с его биографией – если, конечно, возникнет к этому интерес.

А ещё он был человеком сильного духа.

Когда его отца, принца по рождению, жившего во дворце, оклеветал завистливый родственник, возжелавший занять высокое положение при императорском дворе, в результате чего отец оказался в тюрьме, 14-летний Чжу Цзай-юй ушёл из дворца и поселился в землянке. Не впасть в уныние ему помогла страстная любовь к наукам, – чем он и занялся в своём уединении.

Оргáн он, естественно, не мог построить в своей землянке. Но в его распоряжении были флейты и струнный инструмент цитра.

Древнюю китайскую «Систему 12 люй» (для флейт) он изучил очень досконально. С пифагоровой системой (для струн) наверняка тоже был знаком. (Китай давно установил торговые отношения со странами Средиземноморья через Шёлковый путь, а потом – морской.) Оставалось сравнить эти две системы, найти в них то общее, что их объединяет, и… привести их к консонансу.

А общим у этих систем было их астрономическое и математическое происхождение. Только подход к природе звука отличался. У флейт – звук-точка, у струн – звук-волна.

(С подобной двойственностью столкнулись европейские учёные-физики 16-18 веков, когда изучали природу света. Англичанин Исаак Ньютон остался приверженцем корпускулярной теории: свет (фотон) – есть частица-корпускула («точка»), правда, со свойствами волны. Англичанин Томас Юнг доказал, что свет – волна, и даже измерил длины световых волн. А вместе получилась корпускулярно-волновая теория.)

Чжу Цзай-юй создавал «флейтово-струнную» теорию музыкального строя (тоже в своём роде корпускулярно-волновую (не в строгом смысле, конечно, а по подобию), – для звуков).

Пифагорову комму он решил р а в н о м е р н о распределить на все 12 люй (до их повторения на новом витке), а по сути – на 12 квинт (ведь все люй образуются квинтами) и точно зафиксировать полученные высоты звуков. Для этого ему надо было точно рассчитать длины флейтовых труб, – с учётом распределённой между ними коммы.

Это примерно то же, что 365 земных суток разместить в 360 (365˚ в 360˚).

Спираль замкнуть в кольцо, – как мы ощущаем время земного года: всегда с возвратом в одну и ту же точку (Новый год).

Солнечно-лунная пифагорова комма равномерно «растеклась» по 12-ти квинтам (как по 12-ти месяцам земного года). Квинты зазвучали в соответствии с числом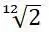

Чжу Цзай-юй нашёл своих очень заинтересованных сторонников не в родном Китае, а в далёкой Европе.

Там над темперацией трудились знаменитые математики – голландец Симон Стевин и француз Марен Мерсенн. Они всё ещё искали свои варианты, как и композитор Андреас Веркмейстер, вдохновлявший И.-С. Баха. Но всё-таки равномерно темперированный строй Чжу Цзац-юя одержал верх. Наверное, из-за своей универсальности. Этот строй стал международным.

…Ты же помнишь, что мы начали эту тетрадь с темы эволюции – то есть «развёртывания» жизни.

Равномерно темперированный строй и стал именно р а з в ё р т ы в а н и е м.

Развёртыванием чего? – Да октавы же!

И тоже – по подобию.

Вот Пифагор с в е р н у л октаву, чтобы получить м и к р о -звуки, виновница которых – комма. Он показал, что подобия уводят в микро-мир, мир тонких материй и энергий, в мир волн и колебаний.

А темперированный строй показал иное подобие. Подобие в сторону увеличения.

Ступень обычной октавы развернулась величиной в саму октаву и, прошагав семь шагов-октав (подобно семи ступеням гаммы-гептатоники), стала величиной в клавиатуру. (Можешь проверить на своей клавиатуре.)

Каждый полутон обычной октавы стал подобием квинты этой же октавы. И 12 этих квинт уместились в семи октавах, – как 12 хроматических ступеней в гамме.

В общем, твоя клавиатура – это огромное подобие октавы (гамма + «хвостик» из оставшихся звуков).

Если к клавиатуре-октаве прибавить ещё одну, и ещё одну, и ещё… – доберёмся до вселенских масштабов!.. Это же мечта оргáна!

Клавиатуры оргáнных мануалов отдают дань особого почтения квинте, этой прародительнице жизни: количество октав каждого мануала – 5, как правило. Но мануалы некоторых оргáнов могут иметь и 5, и 7 октав, – выражая почтение и квинте, и гептатонике (гамме). Музыкальный строй ведь содержит и то и другое.

Если учесть ещё и педаль (ножную клавиатуру) в две октавы с «хвостиком», то в особо величественном оргáне всего октав наберётся от 33 до 37.

То есть, космическому замыслу пифагорова строя оргáн дал развёрнутый – просто гигантский! – масштаб. Представляешь, – каждому из 36-ти звуков и микро-звуков – разворот величиной в целую октаву!

А как же это космическое круженье, которое так прекрасно моделировала струнная кифара? Доступно ли его передать жёстким флейтам-трубам?

О, как изощрённы бывают модуляции человеческой Мысли!

Разрастаясь («развёртываясь»), оргáн покинул поля, где властвовал Пан. Тысячи труб нуждались в особо экономной «упаковке» (как природа экономно «упаковывает» атомы в молекулах и кристаллических решётках сложных образований – веществ, клеток…).

Вариантов этих «упаковок» столько, сколько и самих оргáнов (ты видел на картинках). Они стали архитектурными «организмами». И, как и любой организм, они нуждались в защитной оболочке.

Самой подходящей защитой оказались храмы.

У слова «храм» столько смысловых модуляций – ой-ой-ой!

Самый простой смысл – «дом», наша охрана в жизни. Да и само слово звучит очень близко к «хран» – охрана.

Вариант этого слова – «хорóмы», от «хорóм». Вот в этом варианте появляется смысл «хор» и его модуляция – «гор», гора. Хор – это общность множества голосов, приведённых к согласованности, гармонии:

согласованность человеческих мелодий жизни, а в более широком смысле – жизней всех «тварей» («творений»), населяющих Вселенную. «Гор», «гора» – высота, взлёт, кульминация, доминанта жизни, высшее проявление её сил.

В английском варианте храм – temple. В этом слове намёк на Время в вариациях его быстроты: пространство-время разных скоростей жизни разных творений Вселенной – во взаимной согласованности.

Какие музыкальные смыслы!

Геометрический смысл – куб и сфера: куб самого тела храма, а на сферичность указывает купол. (В проекции на плоскости – это квадрат и круг, и, может быть, намёк на бесконечность известной нам «квадратуры круга». А может быть, «прямоугольное круженье»…)

Вселенная из звуков, помещённая в эту охранную оболочку, стала вести себя в соответствии с моделью настоящей вселенной. Круженье вернулось. Как? – Во многом благодаря полусфере купола.