Арчи Браун - Логические задачи из Зазеркалья
- Название:Логические задачи из Зазеркалья
- Автор:
- Жанр:
- Издательство:Array Литагент Гельветика
- Год:2015
- Город:Санкт-Петербург
- ISBN:978-5-367-03615-2, 978-5-367-03622-0
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Арчи Браун - Логические задачи из Зазеркалья краткое содержание
Логические задачи из Зазеркалья - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
10
Ответ Арчи Брауна
Астра – серого цвета, живет у миссис Бойл; Бонни – черная, живет у миссис Стоун; Сильва – рыжая, живет у мисс Фрог.
Решение
Ниже я привожу три таблицы, где отмечены все утверждения, которые мы можем исключить по условиям задачи. (Например, из первого условия следует, что Бонни – не серая кошка, а из второго, что Сильва – не черная и не серая и т. д). Теперь легко догадаться, какая кошка какой масти и какой хозяйке принадлежит.
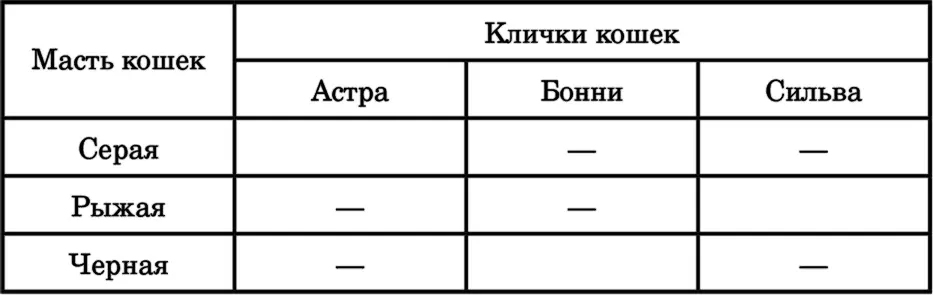
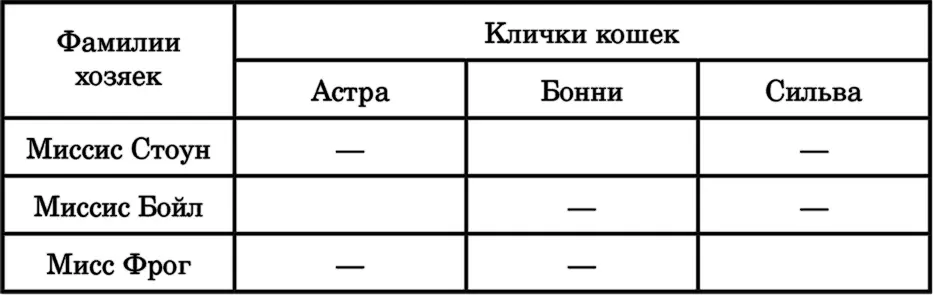
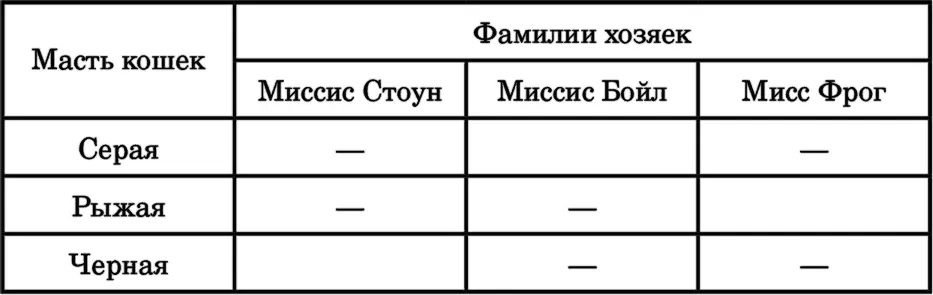
11
Ответ миссис Алисы
Тра – правдив, Тру – лжец.
Решение
Тра никак не мог сказать, что он – лжец. Если бы это было правдой, то получалось бы, что лжец сказал правду. А если бы это было ложью – тогда правдивый дракон солгал. Значит, лжет Тру, а Тра говорит правду.
12
Ответ Арчи Брауна
Дети во второй шкатулке.
Решение
Если верно первое утверждение, значит, верно и второе. А этого по условиям задачи быть не может. Следовательно, первое утверждение неверно, и дети находятся во второй шкатулке.
13
Ответ Арчи Брауна
Письмо было в сумке мистера Томпсона.
Решение
Если ошибся мистер Робинсон, значит, мистер Джексон и мистер Томпсон тоже ошиблись, а это противоречит условиям задачи. Следовательно, мистер Робинсон сказал правду. Значит, ошибся мистер Томпсон, и именно в его сумке нужно было искать письмо.
14
Ответ Арчи Брауна
В белой коробочке – красный и зеленый клубки, в черной – синий и зеленый, в красной – черный и белый клубки, в синей – красный и черный, в зеленой – белый и синий.
Решение
Красный и зеленый клубки могут лежать только в белой коробочке (так как в черной красный клубок лежать не может, согласно условию 4).
Тогда в черной коробочке не могут лежать два зеленых клубка, так как один из них занят. Два синих там тоже не могут быть, иначе нарушится условие 5. Значит, в черной коробочке лежат один зеленый и один синий клубки.
В какой коробочке могут лежать вместе белый и синий клубки? Это не белая, не черная и не синяя коробочки. Условие 2 подсказывает нам, что это – не красная коробочка, значит, остается только зеленая.
У нас остались две коробочки: красная и синяя и четыре клубка: два черных, один белый и один красный.
Красный клубок не может лежать в красной коробочке, а из условия 6 мы знаем, что один из клубков в синей коробочке – черный. Тогда компанию ему составит красный клубок (больше его положить некуда). А в красной коробочке окажутся черный и белый клубки.
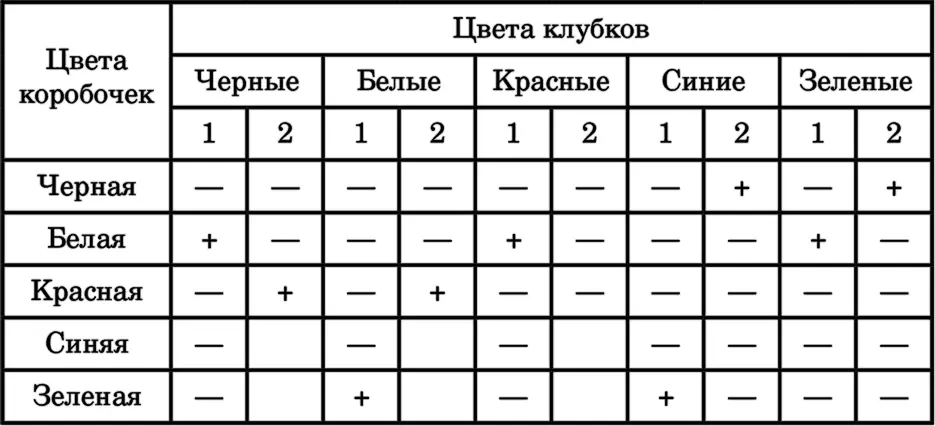
15
Ответ Арчи Брауна
Если Джек проиграл, то Билли выиграл. Значит, он лжет. Но тогда его слова о том, что выиграл Джек, – ложь. Следовательно, Джек не мог проиграть.
Но если Джек выиграл, то он лжет и о правилах игры. Тогда тот, кто проиграл, должен врать, а тот, кто выиграл, должен говорить правду.
Похоже, что внуки решили подшутить над бабушкой.
16
Ответ Арчи Брауна
Никто из людей, названных миссис Алисой, не мог взять роман Диккенса.
Решение
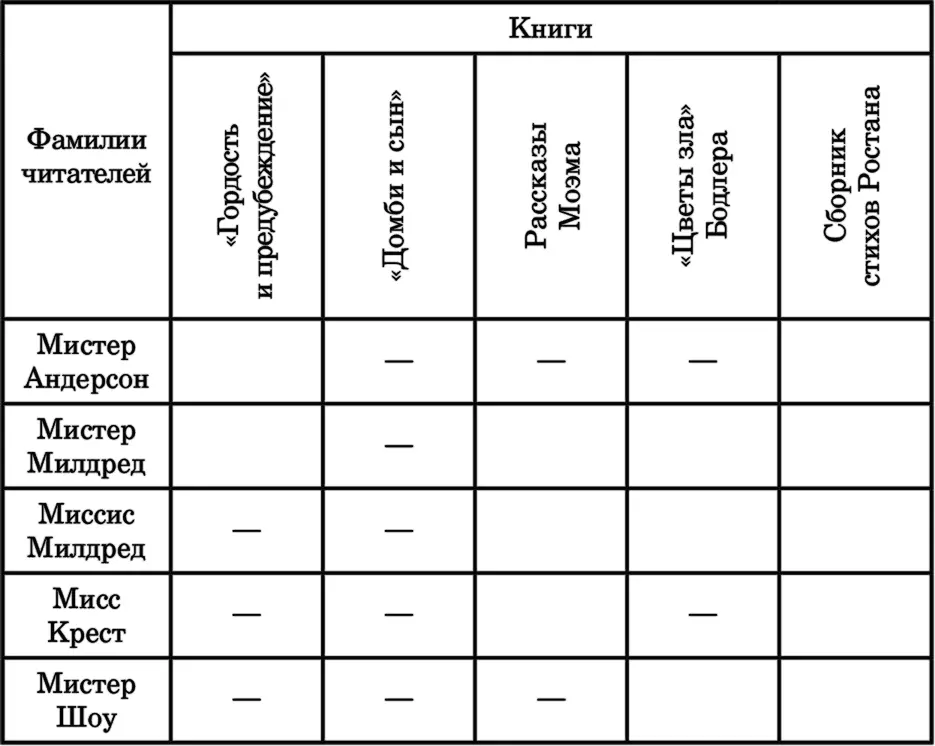
Мистер Милдред уже читал роман «Домби и сын», и ему не понравилось. Миссис Милдред не читает английской литературы. Мисс Крест не читает литературу XIX века, мистер Андерсон читает только романы Джейн Остин и стихи Ростана, а мистер Шоу – только поэзию. Видимо, миссис Алиса что-то вспомнила неправильно.
В таблице приведены факты, которые вспомнила миссис Алиса.
17
Ответ миссис Алисы
Мистер Андерсон читает «Гордость и предубеждение» Джейн Остин; мистер Милдред перечитывает Диккенса; миссис Милдред читает Ростана; мисс Крест выбрала рассказы Моэма; мистер Шоу взял «Цветы зла» Бодлера.
Решение
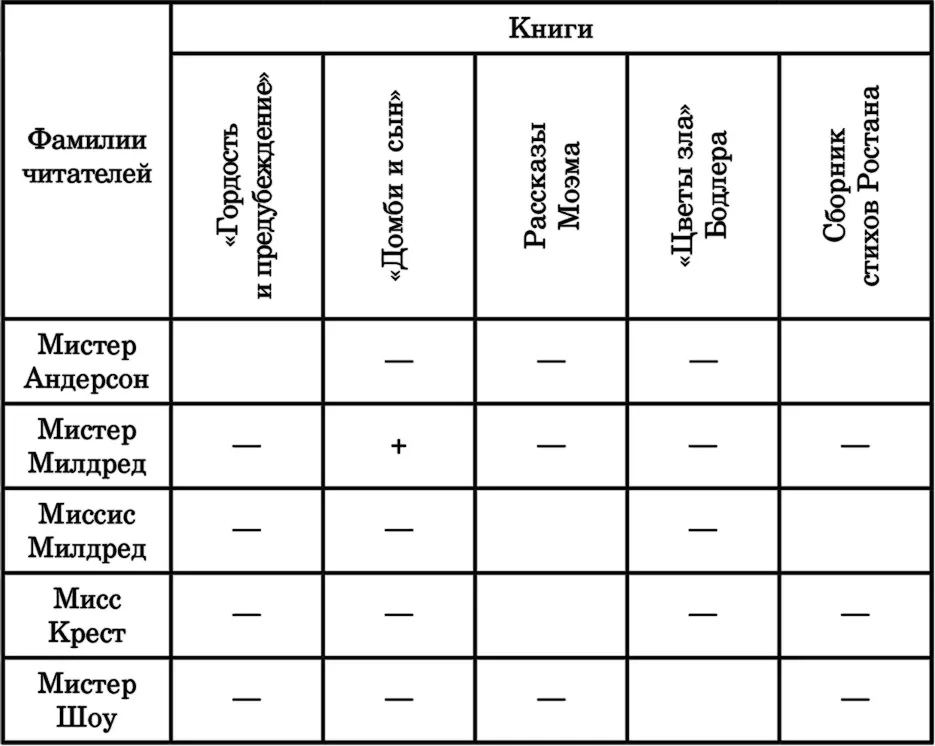
Если миссис Крест не читает Ростана, ей остается только Моэм. Если миссис Милдред не будет читать Бодлера, то из французских авторов ей остается только Ростан (так как Моэма уже заняла мисс Крест). Если мистер Шоу не брал Ростана, значит, он взял Бодлера. В таком случае мистеру Андерсону достается Джейн Остин (так как вторую его любимую книгу уже взяла миссис Милдред), а вот мистер Милдред перечитывает Чарлза Диккенса.
Благодаря новым данным, которые я вспомнила, можно составить следующую таблицу.
18
Ответ Арчи Брауна
Саймон взял «Жизнь и науку», Елена – «Новости литературы», Боб – «Молодежный журнал», Фредерика – «Сады и парки Англии», Алан – «Жизнерадостных ребят», Дороти – «Фильмы, театр и музыку».
Решение
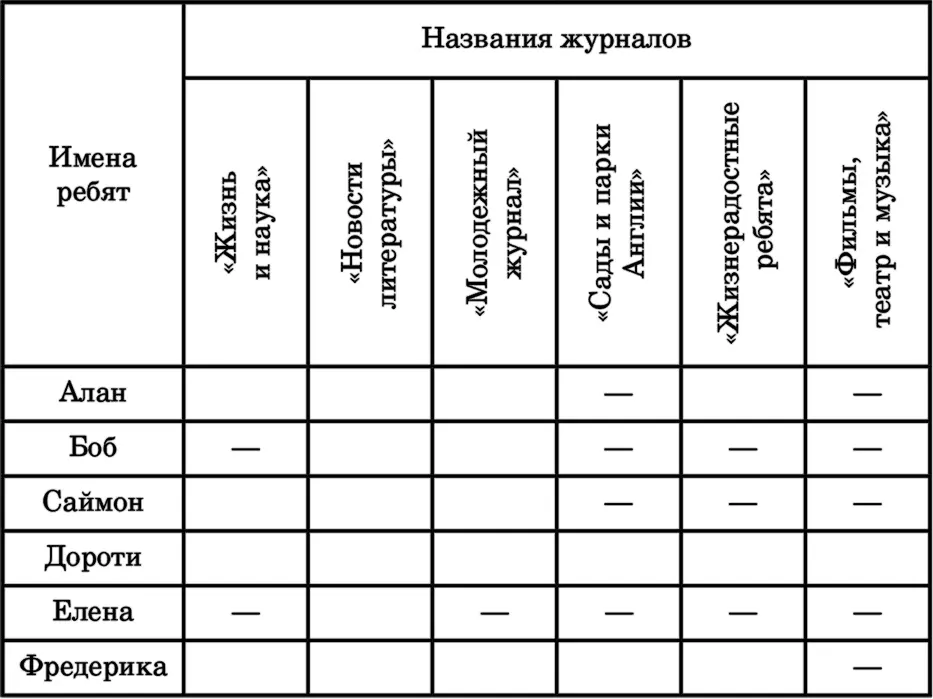
Из условия 1 следует, что ни Алан, ни Боб, ни Саймон не брали «Сады и парки Англии». Елена тоже не брала ни этот журнал, ни «Жизнь и науку». Согласно условию 2, она также не брала «Молодежный журнал», а из условия 3 понятно, что ей ни к чему и «Жизнерадостные ребята», так как этот журнал есть у нее дома. Условие 4 дает нам информацию о том, что ни Елена, ни Фредерика не брали «Фильмы, театр и музыку». Получается, что Елена могла взять только «Новости литературы». А значит, его не брал никто другой из ребят.
Из условия 5 ясно, что Боб не брал «Фильмы, театр и музыку»; из условия 6 – что ни Боб, ни Саймон не брали «Жизнерадостных ребят». Условие 7 утверждает, что Боб не брал «Жизнь и науку», ведь она есть у него дома. Следовательно, Боб мог взять только «Молодежный журнал».
Из условия 8 понятно, что ни Фредерика, ни Алан, ни Саймон не брали в библиотеке журнал «Фильмы, театр и музыка». Значит, его могла взять только Дороти. Тогда Саймону достается «Жизнь и наука», Фредерике – «Сады и парки Англии», а Алану – «Жизнерадостные ребята».
19
Ответы миссис Алисы и Арчи Брауна
Практически во всех вопросах возможны свои варианты ответов. Здесь приводятся лишь примеры.
Ветер (ураган, тайфун и т. д.), фактура, открытие (проблема, гипотеза, теория), кинопленка (память), неудачи (скандалы), тишина, рассказ (болтовня), призма, причина (цель), пар, недостаток (бедность), эхо, решение.
Читать дальшеИнтервал:
Закладка:










