М. Сихов - Тесты и их решения по финансовой математике

Напоминаем, что, если функция накоплений А(t), то ставка доходности в n-ом промежутке определяем следующим образом:

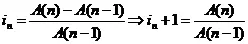. (2.1)

Чтобы определить взвешенную по времени ставку инвестиционной доходности фонда в течение 1989 года, сначала надо определить ставки доходности для каждого промежутка, где известны начальная и конечная стоимости (балансы) фонда, непосредственно предшествующие депозиту или снятию денег. По условию задачи таких промежутков четыре.

Итак, в силу (2.1) ставка доходности с 1 января по 1 апреля 1989 г. определяется уравнением ,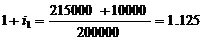

т. к. сразу же после выплаты 31 марта 10000 стоимость портфеля 1 апреля составляет 215000.

С учетом полученного взноса 30 июня 75000 ставка доходности с 1 апреля по 1 июля составляет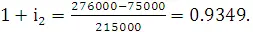

Ставка доходности с 1 июля по 1 октября составляет

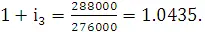
Наконец, ставка доходности с 1 октября по 31 декабря 1989 года равна

.

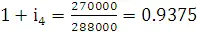Взвешенная по времени доходность за год находится из факторов накопления, соответствующих каждому интервалу, как

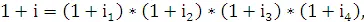(2.2)

т. е. 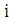=1,125*0.9349*1,0435*0.9375 – 1 = 2.89 %.

(а)=взвешенная по времени ставка инвестиционной доходности фонда в течение 1989 года;

(в)=взвешенная по величине годовая ставка инвестиционной доходности фонда в случае использования простых процентов;

(с)=ставка инвестиционной доходности фонда в случае использования простых процентов и равномерного распределения в течение года всех депозитов и снятий денег.

A. (а)>(в)>(c)

B. (а)>(c)>(в)

С. (с)>(а)>(в)

D. (с)>(в)>(а)

Е. ни один из указанных вариантов

Решение.

Пользуясь (2.1), определим ставки доходности для каждого из 3-х промежутков, соответственно

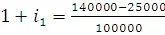=1.15,

,

,

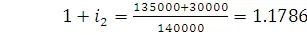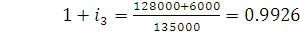Следовательно, в силу (2.2) взвешенная по времени доходность за год будет равна

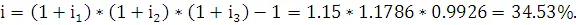
(в) Выведя уравнение стоимости путем сложения всех величин на момент 31 декабря 1989 года, рассчитаем взвешенную по величине доходность фонда в случае использования простых процентов, рассматривая только депозиты и снятия денег и не принимая во внимание промежуточные балансы

.

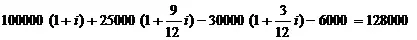Поскольку это уравнение является линейным по i, то легко получить результат

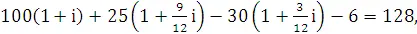
100+100 ,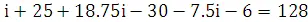

111.25 .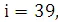

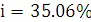(с) Для определения ставку инвестиционной доходности фонда в случае использования простых процентов и равномерного распределения в течение года всех депозитов и снятий денег, предположим, что все депозиты и снятий денег будут происходит в середине года. Тогда выведя уравнение стоимости путем сложения всех величин на момент 31 декабря 1989 года, имеем

100000(1+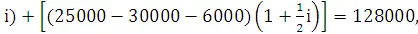

100+100 ,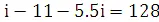

94.5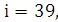

т. е.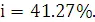

Сравнивая полученные ставки доходности, получим ответ: (с)>(в)>(а).

В каком интервале находится взвешенная по времени ставка доходности за 1989 год ?

A. меньше 6.90%

B. 6.90 %, но меньше 7.30%

C. 7.30 %, но меньше 7.70%

D. 7.70 %, но меньше 8.10%

E. 8.10 % или больше

Решение.

Пользуясь (2.1), определим ставки доходности для каждого из 4-х промежутков, соответственно

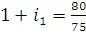=1.067,

,

,

.

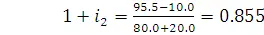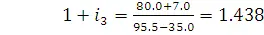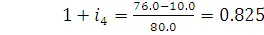Следовательно, взвешенная по времени доходность за год находится из факторов накопления, соответствующих каждому интервалу, как

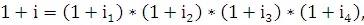
т. е. i=8.2 %.

Рассмотрим следующие данные:

Разовый депозит в фонд: 1000 внесено 1/1/92. Снятия денег из фонда не было.

Процентная ставка в 1992-1993 г.г.: 7 % в год, начисляемых ежемесячно.

Ставка дисконта в 1994-1997 г.г.: 5 % в год , начисляемых ежеквартально.

Интенсивность процента в течение 1998-2002 г.г.: 3 % в год.

Выборочное значение: e =2.71828.

В каком интервале находится величина фонда на 1/1/2003?

A. Меньше 1500

B. 1500, но меньше 1600

C. 1600, но меньше 1700