М. Сихов - Тесты и их решения по финансовой математике

D. 1700, но меньше 1800

E. 1800 или больше

Решение.

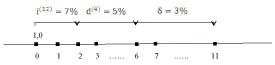
Пусть 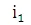– эффективная годовая процентная ставка за 1992-1993 г.г., 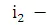за 1994-1997 г.г., 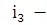за 1998-2002 г.г. Тогда в силу (1.1) накопленная сумма от первоначальной суммы депозита равна

=

=

=

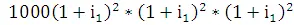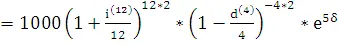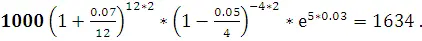
Если 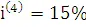, то в каком интервале находится ?

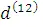A. Меньше 10.95%

B. 10.95 %, но меньше 11.45%

C. 11.45 %, но меньше 11.95%

D. 11.95 %, но меньше 12.45%

E. 12.45 % или больше

Решение.

В силу (1.1)

.

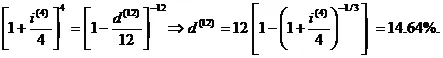Решение на калкуляторе.

Cначала перейдем от ставки 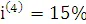к ставке 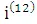по следующей схеме:

.

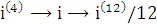1-шаг (расчет 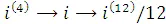): 2 ndICONV; 2 ndCLR WORK; (NOM=) 15 ENTER; ↑(C/Y=) 4 ENTER; ↑(EFF=) CPT: EFF = 15.865;

↓ (C/Y=) 12 ENTER; ↓ (NOM=) CPT: NOM=14.8163; 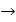/12 =1.2347 %;

Продолжая, в силу (1.2) имеем

2-шаг(расчет 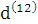): :100 (переход от % к числовому значению); +1=; 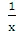(функция деления); 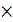14.8163 %=14.64 %.

Решение на компьютере.

1-шаг ( 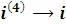): ЭФФЕКТ(Номинальная ставка=15 %; Кол_пер=4)= 15.865 %;

2-шаг ( 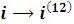): ↓ НОМИНАЛ(Факт_ ставка=14.934 %; Кол_пер=4)= 14.8163 % ;

Далее, силу (1.2) имеем

3-шаг(расчет 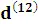): 14.8163 % / (1+14.8163 %/12)=14.64 %.

Первоначальный депозит в фонд: 40000.

Снятия денег из фонда в конце четвертого года: 50000.

Величина фонда в конце восьмого года: 15000.

Других депозитов или снятий денег в течение 8-летнего периода не было.

В каком интервале находится годовая ставка доходности в течение восьмилетнего периода?

A. Меньше 8%

B. 8 %, но меньше 10%

C. 10 %, но меньше 12%

D. 12 %, но меньше 14%

E. 14 % или больше

Решение.

Уравнение стоимости для данного депозита в конечной (8-й) точке имеет вид

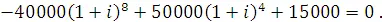
Cледовательно, обозначая 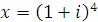и решая при этом полученное квадратное уравнение, находим

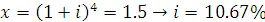
Решение на калкуляторе.

Выше данную диаграмму можно рассматривать как финансовый поток с платежами в конце года

Поэтому пользуясь функцией расчета «Внутренняя ставка доходности (IRR)»

получим

1-шаг(расчет i) :2nd RESET ENTER; CF;

40000 +/– ENTER: CF0= -40000;

↓; 1 ENTER: C01 = 0;

↓; 3 ENTER: F01 = 3;

↓; 50000 ENTER: C02 = 50000;

↓; 1 ENTER: F02 = 1;

↓; 15000 ENTER: C03 = 15000;

↓; 1 ENTER: F03 = 1;

IRR; CPT: IRR= 10.67 %.

Решение на компьютере.

1-шаг(расчет i) :ВСД(-40000; 0; 0; 0; 50000; 0; 0; 0; 15000)= 10.67 %.

Рассмотрим следующие данные:

Дата выдачи ссуды: 01.01.1993.

Сумма ссуды: 6 200.

Дата первого платежа: 31.01.1993.

Частота платежей: ежемесячно.

Количество платежей: 60

Размер каждого из первых: 59 платежей: 100.

Процентная ставка: 9,00 % в год, начисляемых ежемесячно.

В каком интервале находится размер последнего платежа?

A. Меньше 1800

B. 1800, но меньше 2000

C. 2000, но меньше 2200

D. 2200, но меньше 2400

E. 2400 или больше

Решение:

Пусть 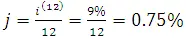и 60-й платеж обозначим через X. Тогда добавляя и отнимая этому платежу платеж в размере 100 и собирая все эти платежи в 60-й точке, имеем

.

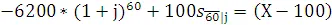Отсюда

= .

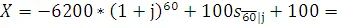
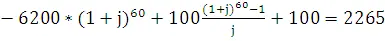Решение на калкуляторе.

1-шаг(расчет X-100): 2nd RESET ENTER; 2nd P/Y 1 ENTER; 2nd QUIT;

60 N; 9/12=0.75 I/Y; -6200 PV; 100 PMT; CPT FV: FV= 2165;

2-шаг(расчет X): +100=2265.

Решение на компьютере.

1-шаг(расчет X-100) :БС(Ставка=9 %/12=0.75 %; Кпер=60; Плт=100; Пс=-6200; Тип=0) = 2165;

2-шаг(расчет X): 2165+100=2265.

Рассмотрим следующие данные:

Дата начала выплат по бессрочному аннуитету: 1/1/91

Процентная ставка: 9 % в год, начисляемых ежегодно

В каком интервале находится стоимость бессрочного аннуитета на 01.01.1991?

A. Меньше 1 050

B. 1 050, но меньше 1 100

C. 1 100, но меньше 1 150

D. 1 150, но меньше 1 200

E. 1 200 или больше

Решение.

Из данной диаграммы нетрудно составить уравнение стоимости для текущей стоимости данного аннуитета

PV= 20 .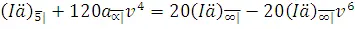

Отсюда, учитывая формулу (см. (3.31) из [1])

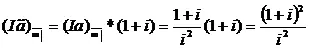
получим