Олег Деревенец - Песни о Паскале

Редкий смельчак сунется в директорский кабинет. Но чтобы вникнуть в предстоящую задачу, нам надо тайно проникнуть к директору школы. Вот вам шапка-невидимка (ещё одна волшебная штуковина), вдохните глубже и ступайте на цыпочках за мной.

Мы находим усталого Семена Семеновича перед кипой исчерканных листков с фамилиями учеников. Чем озабочен директор? Сейчас объясню. В начале учебного года Семен Семенович распорядился, чтобы все ученики вступили в какой-либо кружок или спортивную секцию – по желанию. А теперь, спустя пару месяцев, он проверяет исполнение приказа. Директор намерен наказать тех, кто не исполнил распоряжения, и поощрить состоящих в нескольких кружках или секциях. Но, промучившись неделю со списками кружков, он готов уж отказаться от своей затеи, – задача не поместилась в директорской голове. Судите сами: ведь в школе двести пятьдесят учеников! Спасайте Семена Семеновича!

Директорскую задачу поручим компьютеру, а тому сподручней орудовать с числами. Заменим фамилии учеников числами, назначив каждому ученику уникальный, несовпадающий с другими, номер. Переход от фамилий к номерам и обратно – простая задачка, её мы оставим Семену Семеновичу. Таким образом, наш входной файл со списками учеников будет содержать по одной строке для каждого кружка, где перечисляются через пробел номера учеников, состоящих в этом кружке. Вот пример входного файла для трех кружков.

2 11 4 13

9 17 12 11 3 5 18

14 2 13 15 20

Здесь в первый кружок записались 4 школьника, во второй – 7, а в третий – 5 учеников. Как видите, их номера перечислены в произвольном порядке, что затрудняет ручную обработку таких списков. От компьютера требуется выявить номера учеников (от 1 до 250), которых нет в таком файле. Хочется найти простое решение, а оно возможно лишь с применением нового для нас типа данных – множества.

Слово «множество» намекает на большое количество чего-либо. Чего именно? А все равно! Множества придумали математики, а им безразлично, что считать. Так подать сюда математика, и пусть ответит за всех! Скоро явился математик, взял два кружочка – черный и белый – и, протерев свои толстые очки, стал объяснять. Вот суть его речи.

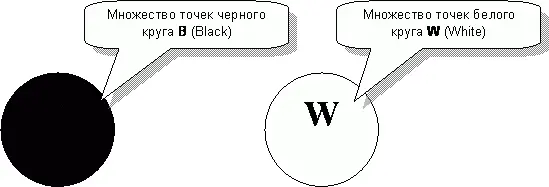
Вы полагаете, что это кружочки? Нет, друзья, это два множества точек, – одно принадлежит черному кругу, другое – белому. Обозначим первое из них латинской буквой B (от Black – «черный»), а второе буквой W (от White – «белый»). Итак, черные и белые точки этих кружков назовём элементами множеств. Сколько там этих точек? Доказано, что бесконечно много, но к свойствам множеств это не имеет отношения. Что же это за свойства?

Добавление к множеству существующих элементов

Покройте черный круг таким же или меньшим черным кругом, или почеркайте его углем, – заметите разницу? Если на белый круг наложить такой же, или почеркать его мелом, – тоже не увидите изменений. Значит, множество не изменится при добавлении к нему элементов, уже входящих в это множество. На языке математики это свойство выразится так:

B + B = B

или так:

W + W + W = W

Не правда ли, странная арифметика?

Объединение множеств

Продолжим наши мысленные опыты и перекрасим оба круга в серый цвет. Будем считать их теперь одной фигурой, разорванной на части.

Так мы получили новое множество, представляющее сумму или объединение двух предыдущих. Обозначим это новое множество буквой G (от Gray – «серый») и выразим то, что сделали, формулой.

G = B + W

Очевидно, что число точек во вновь образованном множестве равно их сумме в двух исходных. Пока в этом нет ничего интересного, – ведь исходные множества B и W, как говорят математики, не пересекаются. Сблизим круги так, чтобы добиться их частичного перекрытия (рис. 82).

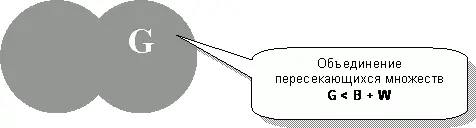
Теперь количество точек в объединенном множестве будет меньше, чем в двух исходных по отдельности.

G < B + W

В общем случае при объединении множеств (как пересекающихся, так и не пересекающихся) соблюдается правило.

G ≤ B + W

Пересечение множеств

Иногда математиков (и не только их) интересует область пересечения множеств, отметим её серым цветом (рис. 83).

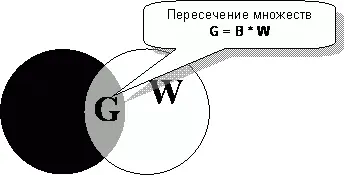
Операцию пересечения множеств обозначают знаком умножения.

G = B • W

Количество точек в пересечении, как понимаете, не может быть больше, чем в любом из исходных множеств B и W. Для этого случая справедливо утверждение: пересечение множеств не больше любого из них.

B • W ≤ B и B • W ≤ W

Вычитание множеств

О солнечных и лунных затмениях слышали все, а кто-то и наблюдал их. Для математика это зримые примеры вычитания множеств; взгляните на рис. 84 – чем не затмения? Серую область можно трактовать как результат вычитания одного круга из другого. На левом рисунке белый круг «отгрыз» часть черного, превратив его в серую область, а на правом – наоборот. Подобающие этим случаям формулы будут таковы.

G = B – W или G = W – B

А если вычитаемый круг окажется больше того, из которого вычитают, и полностью поглотит его? В алгебре разность получится отрицательной, а здесь? Ничего подобного! При вычитании большего множества из меньшего или равного ему получается пустое множество, оно обозначается символом Ø. Из пустого множества тоже можно вычитать, и результатом опять будет пустое множество.

(B – B) – B = Ø

(Ø – W) – B = Ø

Вот такими интересными свойствами обладают множества!

Подмножества и надмножества

На рис. 85 белый круг полностью поглощен черным. Тогда говорят, что множество точек белого круга составляет подмножество точек черного. Или так: множество точек черного круга является надмножеством точек белого. Математик выразит это формулой: