Олег Деревенец - Песни о Паскале

B > W

А если круги совпадают и полностью перекрывают друг друга? Тогда говорят, что множества равны, и любое из них является и подмножеством, и надмножеством другого. В общем случае:

если B ≥ W, то B является надмножеством W;

если B ≤ W, то B является подмножеством W.

Мы рассмотрели несметные множества бесконечно маленьких точек. Но компьютеры ещё не умеют работать с бесконечностями. Так умерим свой аппетит и перейдем к множествам с конечным числом элементов. Поступим так: вместо раскраски кругов расставим на них ряд жирных точек и пронумеруем их числами от 1 до 9 (рис. 86). В ходе последующих опытов нас будут интересовать лишь эти избранные точки (то есть, числа).

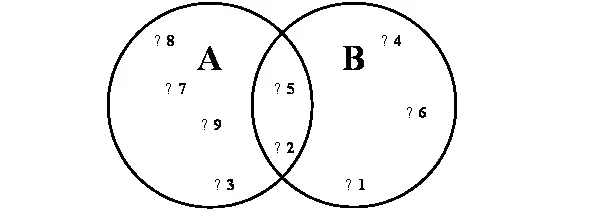
Так мы получили два конечных множества чисел. Одно из них, обозначенное буквой A, содержит числа 8, 7, 9, 3, 5, 2. Другое обозначено буквой B и включает числа 5, 4, 6, 1, 2. Эти множества математики записали бы так:

A = { 8, 7, 9, 3, 5, 2 }

B = { 5, 4, 6, 1, 2 }

Для записи множеств они используют фигурные скобки. Обратите внимание: числа в скобках следуют в произвольном порядке. Это значит, что порядок перечисления элементов множества не важен. Учтите также, что числа 2 и 5 входят в оба множества.

Подобно точкам на круге, каждый элемент числового множества уникален, иными словами, может входить в множество лишь единожды. Вспомните нашу попытку покрасить углем черный круг, – добавление к множеству существующих в нём элементов не изменяет его. Этим же свойством обладают и числовые множества. Например, для нашего случая справедливо следующее.

A + { 8, 7 } = A

Множество A после объединения с множеством {8,7} не изменилось, поскольку уже содержало эти числа.

С числовыми множествами поступают так же, как и с бесконечными: объединяют, пересекают, вычитают и сравнивают. Вот примеры этих операций для нашего случая.

Объединение множеств содержит все числа исходных множеств, при этом повторения (дубликаты) отбрасывают:

G = A + B = { 8, 7, 9, 3, 5, 2 } + { 5, 4, 6, 1, 2 } = { 8, 7, 9, 3, 5, 2, 4, 6, 1 }

Хотя числа 2 и 5 входили в оба исходных множества, в объединении они встречаются по разу.

Пересечение множеств содержит только числа, входящие в оба множества:

A * B = { 8, 7, 9, 3, 5, 2 } * { 5, 4, 6, 1, 2 } = { 5, 2 }

Разность множеств A–B содержит числа, состоящие в множестве A, но отсутствующие в множестве B:

A – B = { 8, 7, 9, 3, 5, 2 } – { 5, 4, 6, 1, 2 } = { 8, 7, 9, 3 }

Разность множеств B–A содержит числа, состоящие в множестве B, но отсутствующие в множестве A:

B – A = { 5, 4, 6, 1, 2 } – { 8, 7, 9, 3, 5, 2 } = { 4, 6, 1 }

Эти «вычисления» легко проверить по рис. 86.

Мощность множества – это наибольшее количество элементов, которое может содержаться в нём. В нашем числовом примере мощность множества равна девяти.

Множество, содержащее все возможные свои элементы, называют полным. В нашем случае полным является объединение множеств A+B.

Множество, содержащее не все возможные элементы, является неполным. Так, множества A и B по отдельности – неполные.

Все это рассказал нам математик. А что же Семен Семенович, или мы забыли о директоре? Нет, конечно, но к директорской задаче мы вернемся после ознакомления с «паскалевскими» множествами.

• Множество – это совокупность различимых объектов (точек, чисел, предметов), которую мы воспринимаем как нечто целое. Отдельные объекты множества называют его элементами.

• К множествам применим ряд операций: объединение, пересечение, вычитание, сравнение.

• Объединение двух множеств содержит по одному элементу из каждого исходного множества.

• Пересечение двух множеств содержит только общие их элементы. Если таких элементов нет, пересечение будет пустым.

• Разность множеств содержит элементы уменьшаемого множества за исключением элементов вычитаемого множества.

• Первое множество является подмножеством второго, если все элементы первого принадлежат второму. И тогда второе множество будет надмножеством первого. Множества совпадают, если содержат одни и те же элементы.

А) Полицейская база данных некоторого государства содержит номера всех автомобилей, сгруппированные в ряд множеств. Три множества составлены по типам автомобилей: легковые, грузовые, автобусы. Шесть множеств образованы по цвету автомобилей: множества белых, черных, желтых, красных, синих и зеленых.

• Пересекается ли множество легковых автомобилей с множеством грузовых? А множество желтых автомобилей с множеством черных?

• Может ли быть непустым пересечение множества желтых автомобилей с множеством автобусов?

• Свидетель дорожно-транспортного происшествия сообщил, что с места преступления скрылся грузовой автомобиль синего цвета. Как вычислить группу подозреваемых автомобилей?

• На улице висит знак: грузовым проезд запрещен. Как определить множество автомобилей, въезд которым разрешен?

Б) Два государства, назовем их A и B, спорят о некой территории, – каждое считает ее своей. Нарисуйте на листочке предполагаемую карту, заштрихуйте спорную область, а затем объясните:

• Как вычислить спорную область государств?

• Как вычислить бесспорную область, включая оба государства?

• Заштрихуйте область, отвечающую формуле G = (A-B) + (B-A).

• Заштрихуйте область, отвечающую формуле G = A+B – A•B. Совпадает ли она с той, что вычислена по предыдущей формуле?

В) Дайте ответы на следующие вопросы.

• Является ли множество ваших одноклассников подмножеством учеников вашей школы?

• Пересекается ли множество ваших друзей с множеством ваших одноклассников?

• Является ли множество ваших друзей подмножеством ваших одноклассников?

Зная силу математических множеств, Никлаус Вирт – «отец» языка Паскаль – ввел в язык тип данных множество и предусмотрел операции с ним.

Элементами множеств здесь могут быть числа, символы и булевы данные – то есть порядковые типы данных размером в один байт. Стало быть, мощность множеств в Паскале не превышает 256.