Олег Деревенец - Песни о Паскале

Один удачливый зверолов в минуту откровенности поделился секретом своих успехов. «Вначале я делю лес своей огромной сетью примерно пополам, и выясняю, в которой из двух половин очутился нужный мне зверь – пояснил охотник. – Затем половину со зверем опять делю пополам и гляжу, где он теперь. И так поступаю, пока животное не окажется в тесном загоне». И зверолов нацарапал на песке рис. 90.

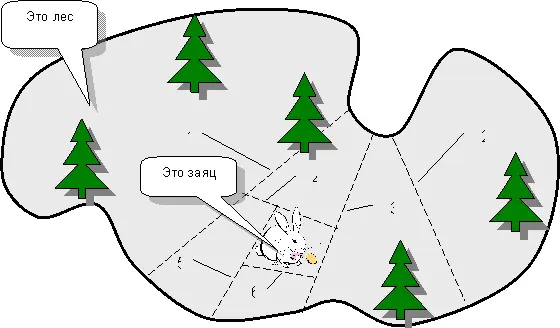
Здесь показано, как шестью сетями (они обозначены цифрами) был изловлен несчастный заяц. Обратите внимание на нумерацию сетей, – они расставлялись в этом порядке.

Не воспользоваться ли уловкой зверолова для поиска в массиве? Ускорит ли это дело? Конечно! Но массив должен быть заранее отсортирован. На рис. 91 показан отсортированный по возрастанию массив, содержащий 12 чисел. Для наглядности числа изображены столбиками. Среди них я выбрал наугад число 32, и прямым перебором нашел его позицию (индекс) в массиве. Очевидно, что я выполнил 8 шагов поиска, поскольку число 32 хранится в 8-м элементе массива.

А теперь применим метод зверолова. Обратимся к среднему элементу массива, индекс которого равен полу-сумме первого и последнего индексов, то есть:

(1+12)/2 = 6

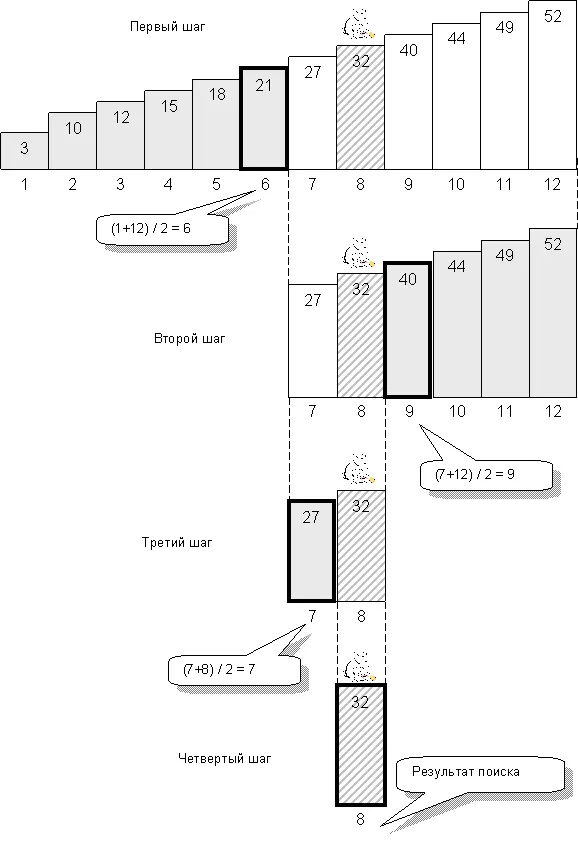
Поскольку индекс – это целое число, дробную часть при делении отбросим. Итак, в позиции 6 оказалось число 21, которое меньше искомого числа 32. Это значит, что «зверь притаился» где-то правее. Раз так, элементы массива, расположенные левее, нас уже не интересуют, – мысленно отбросим их.

С оставшейся частью массива поступим точно так же, то есть, исследуем средний его элемент с индексом

(7+12)/2 = 9

Сравним «живущее» там число 40 с искомым числом 32. На этот раз оно оказалось больше искомого, а значит, искать надо левее, а все, что справа, отбросить. Так, на третьем шаге поиска из 12 элементов массива остались лишь два. Рассуждая тем же порядком, выделяем элемент с индексом

(7+8)/2 = 7

и отбрасываем на этот раз число 27. И вот на последнем четвертом шаге остался лишь один элемент с искомым числом 32.

Подведем итог: вместо 8 шагов последовательного поиска, метод зверолова сделал то же самое за 4 шага. Скажете: всего-то? Восемь шагов или четыре – разница невелика. Так проверим оба метода на большом наборе данных, – поищем в массиве из тысячи чисел. Только избавьте меня от ручной работы, – этот эксперимент поручим компьютеру, для чего соорудим несложную программу.

Частью этой программы будет функция двоичного поиска, алгоритм которой раскрыл зверолов. Но не худо привести и блок-схему этого чудесного изобретения. На блок-схеме (рис. 92), как и в программе, индексы элементов обозначены начальными буквами соответствующих английских слов: L – левый индекс (Left), R – правый индекс (Right), и M – средний индекс (Middle).

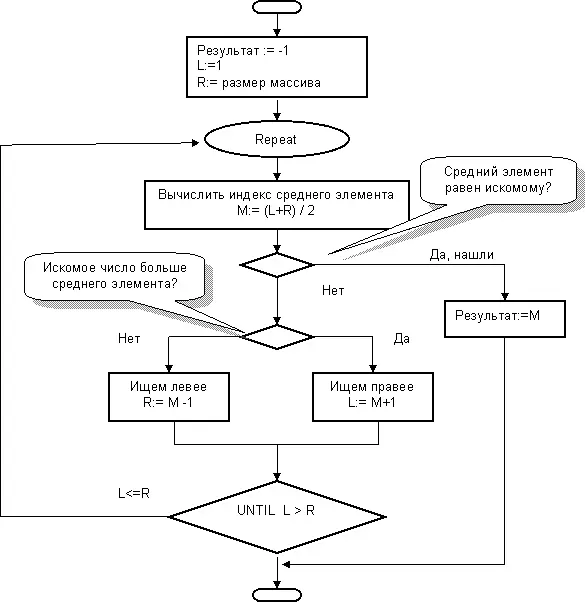
Функцию, работающую по этому алгоритму, я назвал FindBin (Find – «поиск», Binary – «двоичный»), она показана ниже. Полагаю, что приведенных в ней комментариев будет достаточно.

{ Функция двоичного поиска }

function FindBin (aNum: integer): integer;

var L, M, R : integer; { левый, правый и средний индексы }

begin

FindBin:= -1; { результат на случай неудачи }

L:= 1; R:= CSize; { начальные значения индексов }

repeat

M:= (L+R) div 2; { индекс среднего элемента }

if aNum= ArrSort[M] then begin

FindBin:= M; { нашли ! }

Break; { успешный выход из цикла }

end;

if aNum > ArrSort[M] { где искать дальше? }

then L:= M+1 { ищем правее }

else R:= M–1; { ищем левее }

until L > R; { выход при неудачном поиске }

end;

Теперь мы готовы создать исследовательскую программу, которая будет сравнивать два способа поиска.

Поступим так. Объявим два массива по 1000 чисел в каждом. Заполним их случайным образом и один из них отсортируем. Затем сделаем ряд экспериментов, каждый из которых состоит в следующем. Выбрав наугад одно из чисел массива, программа вызовет по очереди две функции: сначала последовательно найдет число в несортированном массиве, а затем двоичным поиском – в сортированном. Поскольку искомое число выбрано из массива, то поиск всегда будет успешным. Затраченные на поиск шаги подсчитаем, и результаты запишем в текстовый файл. После каждого такого эксперимента программа будет ожидать команды пользователя: приняв число ноль, она завершится, а иначе повторит эксперимент.

Подсчет шагов будем вести в глобальной переменной Steps (шаги). Перед вызовом функций поиска она обнуляется, а внутри функций наращивается (эти операторы внутри функций выделены курсивом). Вот и все, полюбуйтесь на эту «экспериментальную установку», введите в компьютер и запустите на выполнение.

{ P_42_1 – Исследование методов поиска }

const CSize = 1000; { размер массива }

{ объявление типа для массива }

Type TNumbers = array [1..CSize] of integer;

Var ArrRand : TNumbers; { несортированный массив }

ArrSort : TNumbers; { сортированный массив }

Steps : integer; { для подсчета числа шагов поиска }

{ Процедура "пузырьковой" сортировки чисел в порядке возрастания }

procedure BubbleSort(var arg: TNumbers);

var i, j, t: Integer;

begin

for i:= 1 to CSize-1 do { внешний цикл }

for j:= 1 to CSize-i do { внутренний цикл }

if arg[j] > arg[j+1] then begin { обмен местами }

t:= arg[j]; arg[j]:= arg[j+1]; arg[j+1]:= t;

end;

end;

{ Функция последовательного поиска (Find Sequence) }

function FindSeq (aNum: integer): integer;

var i: integer;

begin

FindSeq:= -1; { если не найдем, результат будет -1 }

for i:=1 to CSize do begin

Steps:= Steps+1; { подсчет шагов поиска }

if aNum= ArrRand[i] then begin

FindSeq:= i; { нашли, возвращаем позицию }

Break; { выход из цикла }

end;

end;

end;

{ Функция двоичного поиска (Find Binary) }

function FindBin (aNum: integer): integer;

var L, M, R : integer;

begin

FindBin:= -1;