Роман Зыков - Роман с Data Science. Как монетизировать большие данные [litres]

Итак, у нас есть метрика. Теперь с ее помощью мы сможем сравнивать разные модели друг с другом и понимать, какая из них лучше. Можно приступать к обучению.

Практически любая ML-модель для обучения с учителем сводится к двум вещам: определение функции потерь (loss function для одного примера, cost function для множества примеров) и процедуры ее минимизации.

Например, для линейной регрессии это будет среднеквадратичная ошибка в том виде, в каком мы определили ее ранее. Чтобы найти минимум функции потерь, существуют различные процедуры оптимизации. Одна из них называется градиентным спуском (Gradient Descent), она широко применяется на практике.

Как правило, оптимизация выглядит следующим образом:

1. Коэффициенты (которые нужно подобрать) модели инициализируются нулями или случайно.

2. Вычисляется величина функции потерь (например, среднеквадратичное отклонение) и ее градиент (производная от функции потерь). Градиент нам нужен, чтобы понять, куда двигаться для минимизации ошибки.

3. Если функция потерь изменилась существенно и мы не достигли максимального числа повторений расчета, то пересчитаем коэффициенты, исходя из градиента, и идем к шагу 2.

4. Считаем, что оптимизация завершена, возвращаем модель с вычисленными коэффициентами.

Графически градиентный спуск выглядит как на рис. 8.4.

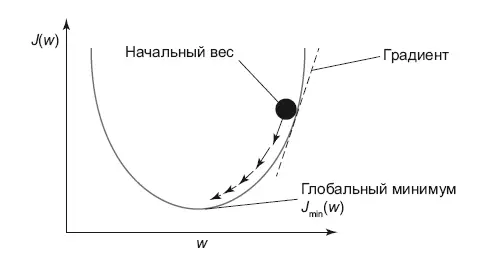
Рис. 8.4.Градиентный спуск

У нас есть функция потерь, и с произвольной точки мы двигаемся в сторону ее минимума последовательно, по шагам.

У этого алгоритма есть еще две версии: стохастический градиентный спуск (SGD) и пакетный (Mini Batch Gradient Descent). Первый используется для работы с большими данными, когда мы из всего датасета используем только один пример для одной итерации обучения. Альтернативной для больших данных является пакетная версия (batch) этого алгоритма, которая вместо одного примера использует подмножество датасета.

Самая простая и популярная модель регрессии. На самом деле ее мы затрагивали в школе, когда писали формулу линейной зависимости. Когда я учился в старших классах, она выглядела так: y = k × x + b . Это так называемая простая линейная регрессия, в ней всего одна независимая переменная.

Обычно работают с множественной линейной регрессией (multivariate linear regression), формула которой выглядит так:

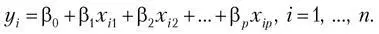
Она состоит из суммы произведений коэффициентов на значение соответствующей фичи и дополнительно свободного члена (intercept). Выглядит она как прямая в случае одной независимой переменной и как гиперплоскость в случае N фич. Когда происходит обучение линейной регрессии, то гиперплоскость строится таким образом, чтобы минимизировать расстояние от точек (из датасета) до нее, что является среднеквадратичным отклонением. Самый первый вопрос, который я задаю кандидатам на должность аналитика данных, звучит так: «У вас есть результат эксперимента, точки отмечены на плоскости с двумя осями. Кто-то провел линию, их аппроксимирующую. Как понять, оптимально ли построена прямая?» Это очень хороший вопрос на понимание сути линейной регрессии.

Если данные на входе линейной регрессии были нормализованы, то чем больше коэффициент у фичи, тем большее влияние на зависимую переменную она оказывает, а значит, и на результат. Положительный коэффициент – увеличение значения фичи увеличивает значение зависимой переменной (положительная корреляция). Отрицательная – это отрицательная корреляция или отрицательная линейная зависимость.

Это самая популярная модель решения задач бинарной (два класса) классификации.

Допустим, у нас есть задача – разделить два класса: крестики и нолики. Я их отметил на координатной сетке, по осям отложил значения фич X1 и X2 (рис. 8.5). Легко видеть, что между крестиками и ноликами можно провести прямую, которая их разделяет. Все, что выше прямой, – нолики, ниже – крестики.

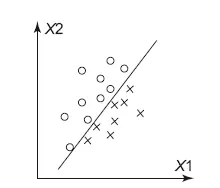
Рис. 8.5.Разделяющая прямая в задаче классификации

Так работает логистическая регрессия – она ищет прямую или гиперплоскость, которая разделяет классы с минимальной ошибкой. Как результат она выдает вероятность принадлежности точки к классу. Чем ближе точка находится к разделяющей поверхности, тем менее модель уверена в своем выборе, вероятность будет приближаться к 0.5, чем дальше точка от поверхности – тем вероятность ближе к 0 или 1, в зависимости от класса. В задаче два класса, поэтому если вероятность принадлежности к одному классу равна 0.3, то ко второму 1–0.3 = 0.7. Для вычисления вероятности в логистической регрессии используется сигмоида (рис. 8.6).

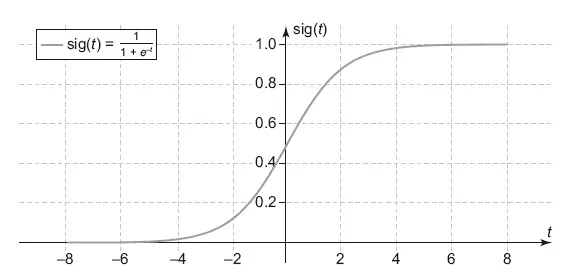
Рис. 8.6.Сигмоида

В этом графике в t подставляется значение из обычной линейной формулы с коэффициентами, как у линейной регрессии. Сама формула является уравнением той разделяющей поверхности, о которой я писал выше.

По популярности это топовая модель как среди исследователей, которые любят ее за простоту и интерпретируемость (коэффициенты такие же, как у линейной регрессии), так и среди инженеров. На очень больших нагрузках, в отличие от других классификаторов, эта простая формула легко масштабируется. И когда вас догоняет в интернете баннерная реклама, скорее всего, за ней стоит логистическая регрессия, которая до недавнего времени использовалась, например, в компании Criteo, одной из самых больших ретаргетинговых компаний в мире [54].

Деревья решения (decision tree) дышат в спину линейным методам по популярности. Это очень наглядный метод (рис. 8.8), который может использоваться для задач классификации и регрессии. Самые лучшие алгоритмы классификации (Catboost, XGboost, Random Forest) основываются на нем. Сам метод нелинейный и представляет собой правила «если…, то…». Само дерево состоит из внутренних узлов и листьев. Внутренние узлы – это условия на независимые переменные (правила). Листья – это уже ответ, в котором содержится вероятность принадлежности к тому или иному классу. Чтобы получить ответ, нужно идти от корня дерева, отвечая на вопросы. Цель – добраться до листа и определить нужный класс.

Дерево строится совсем по иным принципам, чем те, которые мы рассмотрели в линейных методах. Мои дети играют в игру «вопрос-ответ». Один человек загадывает слово, а другие игроки должны с помощью вопросов выяснить его. Допустимые ответы на вопрос только да/нет. Выиграет тот, кто меньшим числом вопросов угадает ответ. С деревом аналогично – начиная от корня дерева, правила строятся таким образом, чтобы за меньшее число шагов дойти до листа.