Роман Зыков - Роман с Data Science. Как монетизировать большие данные [litres]

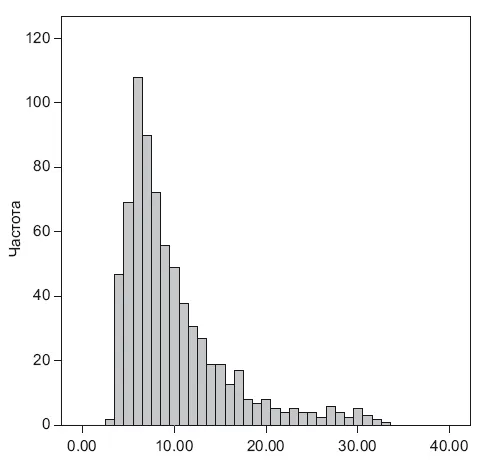
Рис. 10.1.Пример распределения

Возвращать шары нужно, чтобы работать с исходным распределением генеральной совокупности, так как каждое вытягивание будет независимо от предыдущих. Теперь давайте применим интуицию – чем больше шаров мы вытянем, тем лучше распределение выборки будет похоже на распределение в резервуаре, и тем выше точность оценки параметра в выборке мы получим. А сколько нужно вытянуть шаров, чтобы получить приемлемую точность? На этот вопрос уже ответит статистика – об этом чуть позже, а сейчас усложним задачу.

Теперь у нас есть два резервуара, нужно сравнить средний диаметр шаров между ними. Самое время перейти к формулировке гипотезы. Для этого нам понадобится сформулировать основную ( H 0) и альтернативную гипотезу ( H 1) с точки зрения статистики и проведения экспериментов:

• Нулевая гипотеза H 0 (null hypothesis) утверждает, что метрика в эксперименте не изменилась и все наблюдаемые изменения случайны.

• Альтернативная гипотеза H 1 (alternative hypothesis) утверждает, что метрика в эксперименте изменилась, наблюдаемые изменения не случайны.

Тестирование гипотез похоже на суд. Мы считаем, что обвиняемый невиновен, пока не будет найдено строгое доказательство, что он виновен. Аналогично с гипотезами [77], изначально считаем гипотезу H 0 верной, пока не найдем доказательства, чтобы отклонить ее в пользу H 1.

Теперь переформулируем эти общие утверждения для нашей задачи с двумя резервуарами в виде двусторонней гипотезы:

Гипотеза H 0 утверждает, что средние диаметры шаров в обоих резервуарах равны μ1 = μ2.

Гипотеза H 1 утверждает, что диаметры в обоих резервуарах разные —.

Можно также сформулировать в виде односторонней гипотезы:

Гипотеза H 0 утверждает, что средний диаметр в первом резервуаре меньше или равен среднему диаметру во втором резервуаре —.

Гипотеза H 1 утверждает, что средний диаметр в первом резервуаре больше среднего диаметра во втором резервуаре —.

С моей точки зрения, лучше использовать односторонние гипотезы. Ведь проверяя какую-либо идею, мы стремимся улучшить метрику, а значит, нас интересует вопрос, стало ли лучше (гипотеза H 1). Дальше посмотрим, как статистика делает сравнение.

Суд может ошибаться, тестирование статистических гипотез – тоже. Определим эти ошибки с помощью таблицы. Они бывают двух типов (табл. 10.1): ошибка первого рода, когда мы ошибочно отклонили нулевую гипотезу H 0 (признали невиновного виновным), и ошибка второго рода, когда мы ошибочно приняли ее (признали виновного невиновным).

Таблица 10.1. Ошибки статистических гипотез

На языке статистики ошибки описываются вероятностями:

Вероятность ошибки 1-го рода:. Обычно исследователи используют = 0.05 (5 %).

Вероятность ошибки 2-го рода:. Величина (1 —) называется мощностью, которая является вероятностью найти улучшение, если оно есть.

Для упрощения тестирования гипотез Фишер [76] ввел величину p -значение ( p -value), которая является мерой доказательства против нулевой гипотезы H 0. Чем она меньше, тем сильнее доказательства против нулевой гипотезы. Важно заметить, что p -значение – это не вероятность правильности гипотезы H 0, оно работает только для ее отвержения.

В традиционной, или, как я ее называю, фишеровской статистике, p -значение – это универсальное число, которое понятно статистикам и позволяет отвергать нулевую гипотезу. До Фишера использовались конкретные статистики, а не p-значение. Согласно книге Ларри Вассермана «All of Statistics: A Concise Course in Statistical Inference» [77], исследователи обычно используют следующую трактовку p-значения (табл. 10.2) (для = 0.05).

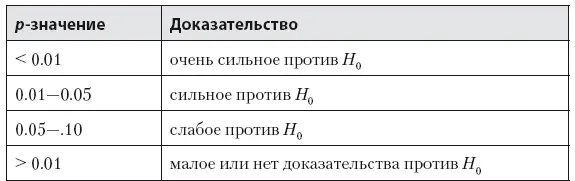
Таблица 10.2. Трактовка p-значений

Теперь посмотрим на графическую интерпретацию двусторонней гипотезы. На рис. 10.2 изображено сравнение распределения нулевой и альтернативной гипотез для нашего примера с двумя резервуарами.

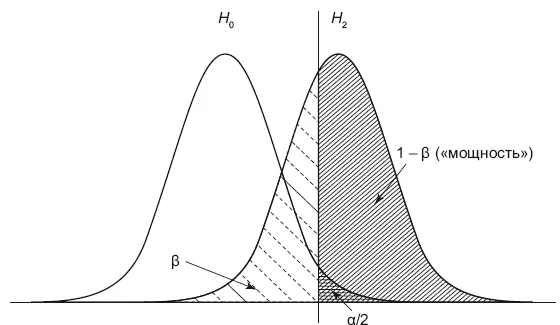
Рис. 10.2.Статистическая мощность

Каждое распределение представляет плотность вероятности. По сути это две гистограммы с площадью под каждой кривой, равной единице. На графике нулевой гипотезы мы отмечаем две вертикальные линии таким образом, что площадь каждой на хвосте была равна /2. В случае односторонней гипотезы строится только одна линия с площадью. Эта линия делит распределение альтернативной гипотезы на две части – и (1 —), площади под ними как раз и равны соответственно ошибке второго рода и мощности критерия. Из графика наглядно видно, что чем дальше находятся пики (средние) этих распределений, тем выше мощность и ниже ошибка второго рода (неверное принятие нулевой гипотезы). И это очень логично – чем дальше средние распределений находятся друг от друга, тем становится явнее разница между гипотезами, а значит, нам легче отвергнуть H 0. С другой стороны, если «уже» распределения, то мощность растет, и нам также легче отвергнуть нулевую гипотезу. Увеличение числа данных в выборке (sample size) способствует «сжиманию» таких распределений.

Именно таким образом работают калькуляторы мощности, которые вычисляют необходимый объем данных для тестов. В калькулятор вводится минимальная детектируемая разность в значениях параметров, уровень и ошибок. На выходе будет объем необходимых данных, которые нужно собрать. Закономерность здесь проста – чем меньшую разницу вы хотите детектировать, тем больше данных для этого нужно.

Альтернативой p -значению является доверительный интервал. Это интервал, внутри которого находится наш измеряемый параметр с определенной степенью точности. Обычно используют 95 %-ную вероятность (= 0.05). Если у нас есть два таких доверительных интервала для тестовой и контрольной группы, то по их пересечению можно понять, есть ли между ними отличие. P-значение и доверительные интервалы – это две стороны одной и той же медали. Интервал удобен для представления данных на графиках. Он часто используется в альтернативных методах оценок А/Б-тестов: байесовской статистике и бутстрэпе.

Как мы уже узнали, p -значение – универсальная метрика тестирования гипотез. Для ее расчета нужно следующее: нулевая гипотеза, статистический критерий, односторонний или двусторонний тест, данные.