Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]

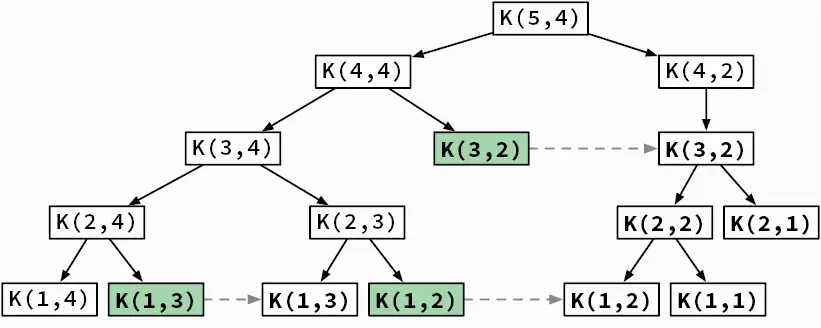
Рис. 3.15.Рекурсивное решение задачи о рюкзаке при помощи мемоизации

Динамическое программирование позволяет добиться от чрезвычайно медленного программного кода приемлемого быстродействия. Тщательно анализируйте свои алгоритмы, чтобы убедиться, что в них нет повторных вычислений. Как мы увидим далее, иногда перекрывающиеся подзадачи могут порождать проблемы.

Дерево рекурсии для функции trade (см. рис. 3.12) не имеет повторных вызовов, и все равно делает повторные вычисления. Он просматривает вход, чтобы найти максимальное и минимальное значения. Затем входные данные разбиваются на две части, и рекурсивные вызовы анализируют их снова, чтобы найти максимум и минимум в каждой половине [42] Вам нужно найти самого высокого мужчину, самую высокую женщину и самого высокого человека в комнате. Будете ли вы измерять рост каждого присутствующего с целью найти самого высокого человека, а затем делать это еще и еще раз применительно к женщинам и мужчинам по отдельности? . Нам нужен другой принцип, для того чтобы избежать этих повторных проходов.

До сих пор мы использовали нисходящий подход, где объем входных данных постепенно уменьшается, пока не будут достигнуты базовые случаи. Но мы также можем пойти снизу вверх : сначала вычислить базовые случаи, а затем раз за разом собирать их, пока не получим общий результат. Давайте решим задачу о лучшей сделке (см. раздел «Полный перебор» ) таким способом.

Пусть P ( n ) — это цена в n -й день, а B ( n ) — лучший день для покупки при продаже в n -й день. Если мы продаем в первый день, то купить у нас получится только тогда же, других вариантов нет, поэтому B (1) = 1. Но если мы продаем во второй день, B (2) может равняться 1 либо 2:

• P (2) < P (1)! B (2) = 2 (купить и продать в день 2);

• P (2) ≥ P (1)! B (2) = 1 (купить в день 1, продать в день 2).

День с самой низкой ценой перед днем 3, но не в день 3 — это B (2). Потому для B (3):

• P (3) < цена в день B (2) —> B (3) = 3.

• P (3) ≥ цена в день B (2) —> B (3) = B (2).

Обратите внимание, что день с самой низкой ценой перед днем 4 будет B (3). Фактически для каждого n день с самой низкой ценой перед днем n — B ( n — 1). Мы можем это использовать, чтобы выразить B ( n) через B ( n — 1):

Когда у нас есть все пары [ n, B ( n )] для для каждого дня n , решением является пара, которая дает самую высокую прибыль. Следующий алгоритм решает задачу, вычисляя все значения B снизу вверх:

function trade_dp(P)

····B[1] ← 1

····sell_day ← 1

····best_profit ← 0

····for each n from 2 to P.length

········if P[n] < P[B[n-1]]

············B[n] ← n

········else

············B[n] ← B[n-1]

········profit ← P[n] — P[B[n]]

········if profit > best_profit

············sell_day ← n

············best_profit ← profit

····return (sell_day, B[sell_day])

Алгоритм выполняет фиксированное число простых операций для каждого элемента входного списка, следовательно, он имеет сложность O ( n). Это огромный рывок в производительности по сравнению со сложностью предыдущего алгоритма O ( n log n) — и совершенно несравнимо со сложностью O ( n 2 ) метода полного перебора. Этот алгоритм также имеет пространственную сложность O ( n) , поскольку вспомогательный вектор B содержит столько же элементов, что и входные данные. Из приложения IV вы узнаете, как сэкономить память за счет создания алгоритма с пространственной сложностью O (1).

Многие задачи связаны с минимизацией или максимизацией целевого значения: найти кратчайший путь, получить наибольшую прибыль и т. д. Такие задачи называются задачами оптимизации . Когда решением является последовательность вариантов, мы часто используем стратегию ветвей и границ . Ее цель состоит в том, чтобы выиграть время за счет быстрого обнаружения и отбрасывания плохих вариантов. Чтобы понять, каким образом они ищутся, мы сначала должны разобраться в понятиях «верхняя граница» и «нижняя граница».

Границы обозначают диапазон значения. Верхняя граница устанавливает предел того, каким высоким оно может быть. Нижняя граница — это наименьшее значение, на которое стоит надеяться; она гарантирует, что любое значение либо равно ей, либо ее превышает.

Мы порой легко находим решения, близкие к оптимальным: короткий путь — но, возможно, не самый короткий; большая прибыль — но, возможно, не максимальная. Они дают границы оптимального решения. К примеру, любой короткий маршрут из одной точки в другую никогда не будет короче расстояния между ними по прямой. Следовательно, расстояние по прямой является нижней границей самого короткого пути.

В задаче о жадном грабителе и рюкзаке (см. раздел «Эвристические алгоритмы» ) прибыль, полученная посредством greedy_knapsack, является нижней границей оптимальной прибыли (она может быть или не быть близкой к оптимальной прибыли). Теперь представим версию задачи о рюкзаке, в которой вместо предметов у нас сыпучие материалы, и мы можем насыпать их в рюкзак, сколько поместится. Эта версия задачи решается «жадным» способом: просто продолжайте насыпать материалы с самым высоким соотношением стоимости и веса:

function powdered_knapsack(items, max_weight)

····bag_weight ← 0

····bag_items ← List.new

····items ← sort_by_value_weight_ratio(items)

····for each i in items

········weight ← min(max_weight — bag_weight,

·····················i.weight)

········bag_weight ← bag_weight + weight

········value ← weight * i.value_weight_ratio

········bagged_value ← bagged_value + value

········bag_items.append(item, weight)

····return bag_items, bag_value

Добавление ограничения неделимости предметов только уменьшит максимально возможную прибыль, потому что нам придется менять последнюю уложенную в рюкзак вещь на что-то подешевле. Это означает, что powdered_knapsack дает верхнюю границу оптимальной прибыли с неделимыми предметами [43] Метод удаления ограничений из задач называется ослаблением . Он часто используется для вычисления ограничений в задачах оптимизации. .