Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]
- Название:Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]
- Автор:
- Жанр:
- Издательство:Питер
- Год:2018
- Город:СПб.
- ISBN:978-5-4461-0587-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику] краткое содержание
Владстон Феррейра Фило знакомит нас с вычислительным мышлением, позволяющим решать любые сложные задачи. Научиться писать код просто — пара недель на курсах, и вы «программист», но чтобы стать профи, который будет востребован всегда и везде, нужны фундаментальные знания. Здесь вы найдете только самую важную информацию, которая необходима каждому разработчику и программисту каждый день. cite
Владстон Феррейра Фило
Теоретический минимум по Computer Science [Все что нужно программисту и разработчику] - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Убедитесь сами: напишите алгоритмы сортировки с линейно-логарифмической и квадратичной сложностью, а затем сравните их эффективность на примере случайных списков разного размера. Когда объемы входных данных огромны, такие улучшения часто оказываются необходимы.
А теперь давайте разделим и осилим задачи, в отношении которых мы раньше применяли полный перебор.
| Объем данных | Квадратичный | Логлинейный |
|---|---|---|
| 196 (число стран в мире) | 38 мс | 2 с |
| 44 000 (число аэропортов в мире) | 32 минуты | 12 минут |
| 171 000 (число слов в словаре английского языка) | 8 часов | 51 минута |
| 1 млн (число жителей Гавайев) | 12 дней | 6 часов |
| 19 млн (число жителей штата Флорида) | 11 лет | 6 дней |
| 130 млн (число книг, опубликованных за все время) | 500 лет | 41 день |
| 4,7 млрд (число страниц в Интернете) | 700 000 лет | 5 лет |
Разделить и заключить сделку
Для задачи о самой лучшей сделке (см. раздел «Полный перебор»  ) подход «Разделяй и властвуй» оказывается лучше, чем решение «в лоб». Разделение списка цен пополам приводит к двум подзадачам: нужно найти лучшую сделку в первой половине и лучшую сделку во второй. После этого мы получим один из трех вариантов:
) подход «Разделяй и властвуй» оказывается лучше, чем решение «в лоб». Разделение списка цен пополам приводит к двум подзадачам: нужно найти лучшую сделку в первой половине и лучшую сделку во второй. После этого мы получим один из трех вариантов:
1) лучшая сделка с покупкой и продажей в первой половине;
2) лучшая сделка с покупкой и продажей во второй половине;
3) лучшая сделка с покупкой в первой половине и продажей во второй.
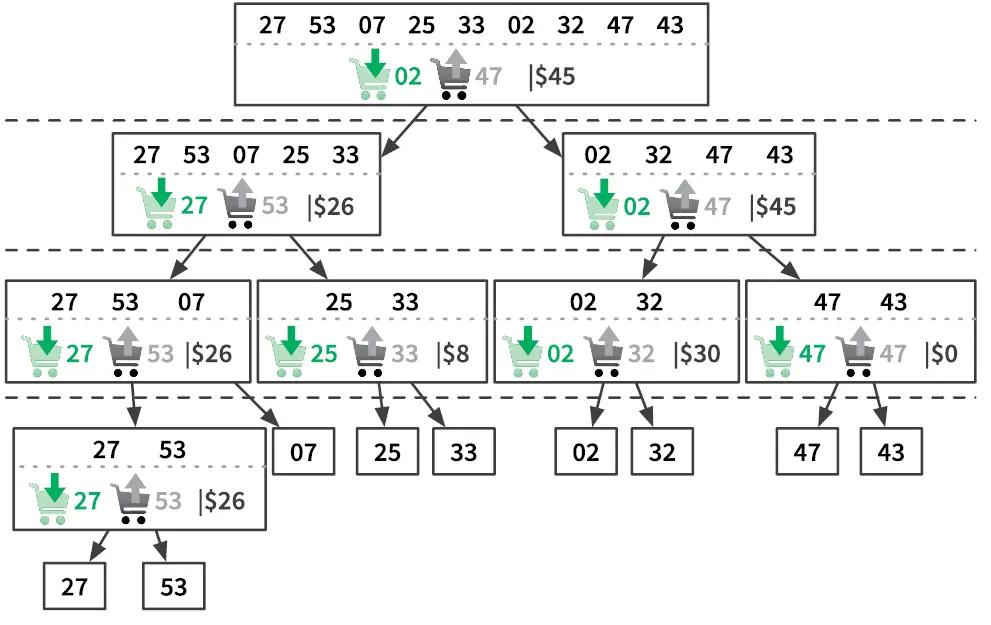
Рис. 3.12.Демонстрация выполнения функции trade. Прямоугольники показывают отдельные вызовы trade с входными и выходными данными
Первые два случая — это решения подзадач. Третий легко находится: нужно найти самую низкую цену в первой половине списка и самую высокую во второй. Если на входе данные всего за один день, то единственным вариантом становится покупка и продажа в этот день, что приводит к нулевой прибыли.
function trade(prices)
····if prices.length = 1
········return 0
····former ← prices.first_half
····latter ← prices.last_half
····case3 ← max(latter) — min(former)
····return max(trade(former), trade(latter), case3)
Функция trade выполняет тривиальное сравнение, разбивает список пополам и находит максимум и минимум в его половинах. Поиск максимума или минимума в списке из n элементов требует просмотра всех n элементов, таким образом, отдельный вызов trade стоит O ( n ).
Вы наверняка заметите, что дерево рекурсивных вызовов функции trade (рис. 3.12) очень похоже на такое же для сортировки слиянием (рис. 3.11). Оно тоже имеет log 2 n шагов разбиения, каждый стоимостью O ( n ). Следовательно, функция trade тоже имеет сложность O ( n log n ) — это огромный шаг вперед по сравнению со сложностью O ( n 2) предыдущего подхода, основанного на полном переборе.
Разделить и упаковать
Задачу о рюкзаке (см. раздел «Полный перебор»  ) тоже можно разделить и тем самым решить. Если вы не забыли, у нас n предметов на выбор. Мы обозначим свойство каждого из них следующим образом:
) тоже можно разделить и тем самым решить. Если вы не забыли, у нас n предметов на выбор. Мы обозначим свойство каждого из них следующим образом:
• w i— это вес i -го предмета;
• v i— это стоимость i- го предмета.
Индекс i предмета может быть любым числом от 1 до n . Максимальный доход для вместимости c рюкзака с уже выбранными n предметами составляет K ( n, c ). Если рассматривается дополнительный предмет i = n + 1, то он либо повысит, либо не повысит максимально возможный доход, который становится равным большему из двух значений.
1. K ( n, c ) — если дополнительный предмет не выбран.
2. K ( n, c − w n+1) + v n+1— если дополнительный предмет выбран.
Случай 1 предполагает отбраковку нового предмета, случай 2 — включение его в набор и размещение среди выбранных ранее вещей, обеспечивая для него достаточное пространство. Это значит, что мы можем определить решение для n предметов как максимум частных решений для n — 1 предметов:
K ( n, c ) = max ( K ( n − 1, c ),
K ( n − 1, c − w n) + v n).
Вы уже достаточно знаете и должны легко преобразовать эту рекурсивную формулу в рекурсивный алгоритм. Рисунок 3.13 иллюстрирует, как рекурсивный процесс решает задачу. На схеме выделены одинаковые варианты — они представляют идентичные подзадачи, вычисляемые более одного раза. Далее мы узнаем, как предотвратить такие повторные вычисления и повысить производительность.
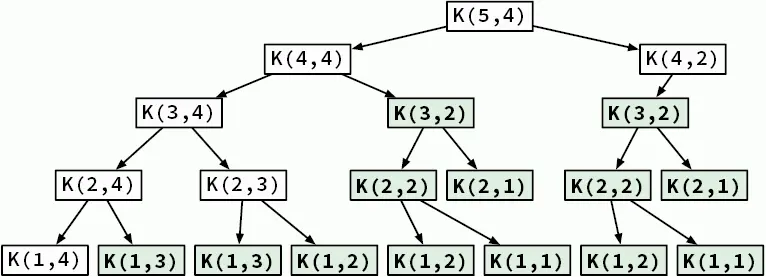
Рис. 3.13.Решение задачи о рюкзаке с 5 предметами и вместимостью рюкзака 4. Предметы под номерами 5 и 4 весят две единицы, остальные — одну единицу
3.7. Динамическое программирование
Во время решения задачи иногда приходится выполнять одни и те же вычисления многократно [41] В таком случае говорят, что задачи имеют перекрывающиеся подзадачи.
. Динамическое программирование позволяет идентифицировать повторяющиеся подзадачи, чтобы можно было выполнить каждую всего один раз. Общепринятый метод, предназначенный для этого, основан на запоминании и имеет «говорящее» название. 
Мемоизация Фибоначчи
Помните алгоритм вычисления чисел Фибоначчи? Его дерево рекурсивных вызовов (см. рис. 3.3) показывает, что fib(3) вычисляется многократно. Мы можем это исправить, сохраняя результаты по мере их вычисления и делая новые вызовы fib только для тех вычислений, результатов которых еще нет в памяти (рис. 3.14). Этот прием
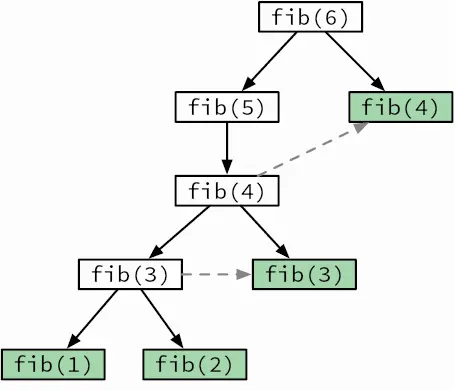
Рис. 3.14.Дерево рекурсивных вызовов для dfib. Зеленые прямоугольники обозначают вызовы, не выполняемые повторно
многократного использования промежуточных результатов называется мемоизацией . Он повышает производительность функции fib:

Мемоизация предметов в рюкзаке
Очевидно, что в дереве рекурсивных вызовов для задачи о рюкзаке (см. рис. 3.13) имеются многократно повторяемые вызовы. Применение того же самого приема, который мы использовали для функции Фибоначчи, позволяет избежать этих повторных вызовов и в итоге уменьшить объем вычислений (рис. 3.15).
Читать дальшеИнтервал:
Закладка:
![Обложка книги Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]](/books/1060455/vladston-ferrejra-filo-teoreticheskij-minimum-po-co.webp)









