Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]
- Название:Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]
- Автор:
- Жанр:
- Издательство:Питер
- Год:2018
- Город:СПб.
- ISBN:978-5-4461-0587-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику] краткое содержание
Владстон Феррейра Фило знакомит нас с вычислительным мышлением, позволяющим решать любые сложные задачи. Научиться писать код просто — пара недель на курсах, и вы «программист», но чтобы стать профи, который будет востребован всегда и везде, нужны фундаментальные знания. Здесь вы найдете только самую важную информацию, которая необходима каждому разработчику и программисту каждый день. cite
Владстон Феррейра Фило
Теоретический минимум по Computer Science [Все что нужно программисту и разработчику] - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
2. Повторять, пока все поселки не будут подключены.
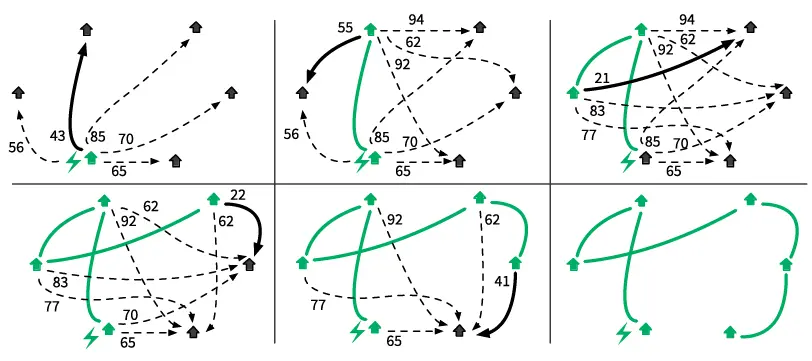
Рис. 3.10.Решение задачи об электрической сети с «жадными» вариантами выбора
На каждом шаге мы выбираем для соединения пару поселков, которая на текущий момент выглядит самой лучшей. Несмотря на то что мы не анализируем, как этот вариант влияет на будущие возможности выбора, присоединение самого близкого поселка без электричества — всегда правильный выбор. Здесь нам повезло: структура задачи идеально подходит для решения «жадным» алгоритмом. В следующем разделе мы увидим структуры задач, для решения которых нужна стратегия великих полководцев.
3.6. Разделяй и властвуй
Когда силы врага раздроблены на небольшие группы, его проще победить. Цезарь и Наполеон управляли Европой, разделяя и завоевывая своих врагов. При помощи той же стратегии вы можете решать задачи — в особенности задачи с оптимальной подструктурой , то есть такие, которые легко делятся на подобные, но меньшие подзадачи. Их можно дробить снова и снова, пока подзадачи не станут простыми. Затем их решения объединяются — так вы получаете решение исходной задачи.
Разделить и отсортировать
Если у нас есть большой список, который нужно отсортировать, мы можем разделить его пополам: каждая половина становится подзадачей сортировки. Затем решения подзадач (то есть отсортированные половины списка) можно объединить в конечное решение при помощи алгоритма слияния [37] Это самый первый алгоритм, который вы увидели в главе 3.
. Но как отсортировать эти две половины? Их тоже можно разбить на подзадачи, отсортировать и объединить.
Новые подзадачи будут также разбиты, отсортированы и объединены. Процесс разделения продолжаем, пока не достигнем базового случая: списка из одного элемента. Такой список уже отсортирован!
Этот изящный рекурсивный алгоритм называется сортировкой слиянием . Как и для последовательности Фибоначчи (см. раздел «Рекурсия»), дерево рекурсивных вызовов помогает увидеть, сколько раз функция merge_sort вызывает саму себя (рис. 3.11).
function merge_sort(list)
····if list.length = 1
········return list
····left ← list.first_half
····right ← list.last_half
····return merge(merge_sort(left),
·················merge_sort(right))
Теперь давайте найдем временную сложность сортировки слиянием. Для этого сначала подсчитаем операции, выполняемые на каждом отдельном шаге разбиения, а затем — общее количество шагов.
Подсчет операций.Допустим, у нас есть большой список размером n. При вызове функция merge_sort выполняет следующие операции:
• разбивает список на половины, что не зависит от размера списка O (1);
• вызывает функцию merge (из раздела «Итерация» мы знаем, что merge имеет сложность O ( n );
• делает два рекурсивных вызова merge_sort, которые не учитываются [38] Операции, которые выполняются рекурсивными вызовами, подсчитываются на следующем шаге разбиения.
.
Поскольку мы оставляем только доминирующий член и не учитываем рекурсивные вызовы, временная сложность функции составляет O ( n ). Теперь подсчитаем временную сложность каждого шага разбиения.
Шаг разбиения 1.Функция merge_sort вызывается для списка из n элементов. Временная сложность этого шага составляет O ( n ).
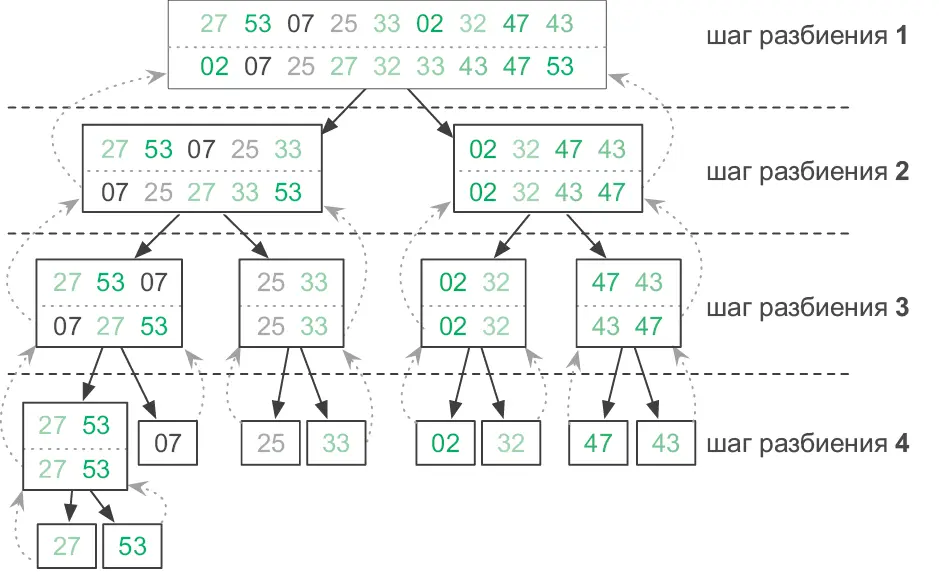
Рис. 3.11.Демонстрация сортировки слиянием. Прямоугольники показывают отдельные вызовы merge_sort, при этом входные данные находятся вверху, а выходные — внизу
Шаг разбиения 2.Функция merge_sort вызывается дважды, каждый раз для 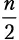 элементов. Мы получаем
элементов. Мы получаем 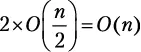 .
.
Шаг разбиения 3.Функция merge_sort вызывается четыре раза, каждый раз для 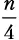 элементов:
элементов: 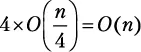 .
.
.
.
.
.
Шаг разбиения x.Функция merge_sort вызывается 2 xраз, каждый для списка из 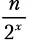 элементов:
элементов: 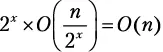 .
.
Все шаги разбиения имеют одинаковую сложность O ( n ). Временная сложность сортировки слиянием, следовательно, составляет x × O ( n ), где x — это количество шагов разбиения, необходимых для полного выполнения алгоритма [39] Мы не можем проигнорировать x , потому что это не константа. Если размер списка n удвоится, то нам потребуется еще один шаг разбиения. Если n увеличится в четыре раза, тогда нужны будут два дополнительных шага разбиения.
.
Подсчет шагов.Как вычислить x ? Мы знаем, что рекурсивные функции заканчивают вызывать себя, как только достигают своего базового случая. Наш базовый случай — это одноэлементный список. Мы также увидели, что шаг разбиения x работает на списках из 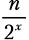 элементов. Потому:
элементов. Потому:
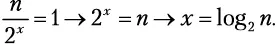
Если вы не знакомы с функцией log 2, то не робейте! x = log 2 n — это просто еще один способ написать 2 x= n . Программисты любят логарифмический рост.
Посмотрите, как медленно растет количество требуемых шагов разбиения [40] Любой процесс, постепенно сокращающий объем входных данных на каждом шаге, деля его на постоянный делитель, требует логарифмического количества шагов до полного сокращения входных данных.
с увеличением общего числа сортируемых элементов (табл. 3.1).
| Размер списка ( n ) | log2 n | Требуемое количество шагов разбиения |
|---|---|---|
| 10 | 3,32 | 4 |
| 100 | 6,64 | 7 |
| 1024 | 10,00 | 10 |
| 1 000 000 | 19,93 | 20 |
| 1 000 000 000 | 29,89 | 30 |
Временная сложность сортировки слиянием, следовательно, составляет log 2 n × O ( n ) = O ( n log n ). Это колоссальное улучшение по сравнению с сортировкой выбором O ( n 2). Помните разницу в производительности между линейно-логарифмическими и квадратичными алгоритмами, которые мы видели в предыдущей главе на рис. 2.4? Даже если предположить, что алгоритм O ( n 2) будет обрабатываться быстрым компьютером, в конечном счете он все равно окажется медленнее, чем алгоритм O ( n log n ) на слабой машине (табл. 3.2).
Читать дальшеИнтервал:
Закладка:
![Обложка книги Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]](/books/1060455/vladston-ferrejra-filo-teoreticheskij-minimum-po-co.webp)









