Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]

Итеративная стратегия состоит в использовании циклов (например, for и while) для повторения процесса до тех пор, пока не окажется соблюдено некое условие. Каждый шаг в цикле называется итерацией . Итерации очень полезны для пошагового просмотра входных данных и применения одних и тех же операций к каждой их порции. Вот пример.

Объединение списков рыб У вас есть списки морских и пресноводных рыб, оба упорядочены в алфавитном порядке. Как создать из них один общий список, тоже отсортированный по алфавиту?

Мы можем сравнивать в цикле верхние элементы двух списков (рис. 3.1).

Данный процесс можно записать в виде одного цикла с условием продолжения while loop:

function merge(sea, fresh)

····result ← List.new

····while not (sea.empty and fresh.empty)

········if sea.top_item > fresh.top_item

············fish ← sea.remove_top_item

·······else

···········fish ← fresh.remove_top_item

·····result.append(fish)

return result

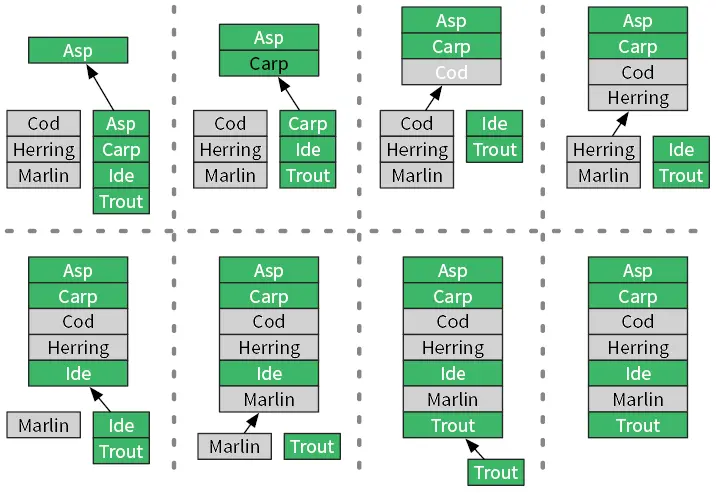
Рис. 3.1.Объединение двух отсортированных списков в третий, тоже отсортированный

Он выполняет обход всех названий рыб из входных списков, совершая фиксированное число операций для каждого элемента [28] Объем входных данных (так называемый размер входа) — это число элементов в обоих входных списках, взятых вместе. Цикл while выполняет три операции для каждого из этих элементов, следовательно, T( n ) = 3 n . . Следовательно, алгоритм слияния merge имеет сложность O ( n ).

В предыдущей главе мы увидели, как функция сортировки выбором selection_sort использует один цикл, вложенный в другой. Сейчас мы научимся использовать вложенный цикл для вычисления степенного множества . Если дана коллекция объектов S, то степенное множество S есть множество, содержащее все подмножества S [29] Если вам нужно больше узнать о множествах, см. приложение III. .

Исследование запахов В парфюмерии цветочные ароматы изготавливают путем комбинирования запахов различных цветов. Если дано множество цветов F , то как посчитать все ароматы, которые можно изготовить из них?

Любой аромат состоит из подмножества F , потому его степенное множество содержит все возможные ароматы. Это степенное множество вычисляется итеративно. Для нулевого множества цветов есть всего один вариант — без запаха. В случае, когда мы берем очередной цветок, мы дублируем уже имеющиеся ароматы и добавляем его к ним (рис. 3.2).

Этот процесс можно описать при помощи циклов. Во внешнем цикле мы принимаем решение, какой цветок будем рассматривать следующим. Внутренний цикл дублирует ароматы и добавляет новый цветок к этим копиям.

function power_set(flowers)

····fragrances ← Set.new

····fragrances.add(Set.new)

····for each flower in flowers

········new_fragrances ← copy(fragrances)

········for each fragrance in new_fragrances

············fragrance.add(flower)

········fragrances ← fragrances + new_fragrances

····return fragrances

Добавление каждого нового цветка приводит к удвоению количества ароматов в множестве fragrances, что говорит об экспоненциальном росте (2 k+1= 2 × 2 k). Алгоритмы, которые удваивают число операций, если объем входных данных увеличивается на один элемент, — экспоненциальные, их временная сложность — O (2 n).

Генерирование степенных множеств эквивалентно генерированию таблиц истинности (см. раздел «Логика» в главе 1). Если обозначить каждый цветок логической переменной, то любой аромат легко представить в виде значений True/False этих переменных. В таблице истинности каждая строка будет возможной формулой аромата.

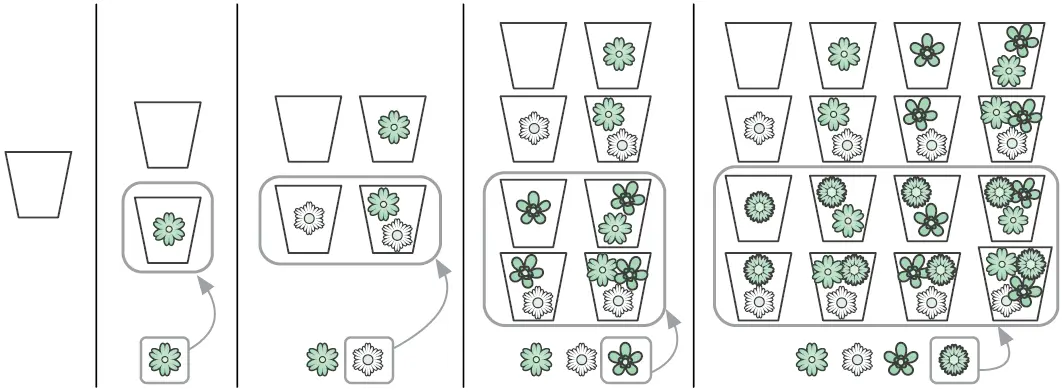
Рис. 3.2.Итеративное перечисление всех ароматов с использованием четырех цветков

Мы говорим о рекурсии , когда функция делегирует работу своим клонам. Рекурсивный алгоритм естественным образом приходит на ум, когда нужно решить задачу, сформулированную с точки зрения самой себя. Например, возьмем известную последовательность Фибоначчи. Она начинается с двух единиц, и каждое последующее число является суммой двух предыдущих: 1, 1, 2, 3, 5, 8, 13, 21. Как создать функцию, возвращающую n -е число Фибоначчи (рис. 3.3)?

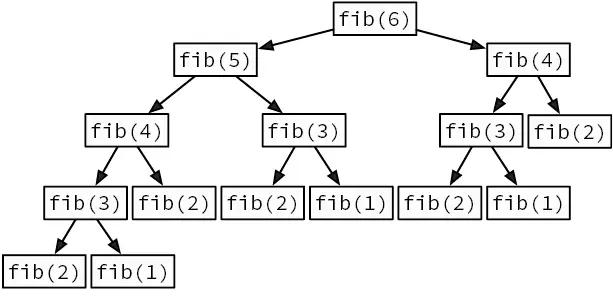
Рис. 3.3.Рекурсивное вычисление шестого числа Фибоначчи

function fib(n)

····if n ≤ 2

········return 1

····return fib(n — 1) + fib(n — 2)

При использовании рекурсии требуется творческий подход, чтобы понять, каким образом задача может быть поставлена с точки зрения самой себя. Чтобы проверить, является ли слово палиндромом [30] Палиндромы — это слова и фразы, которые читаются одинаково в обе стороны, например «Ада», «топот», «ротатор». , нужно посмотреть, изменится ли оно, если его перевернуть. Это можно сделать, проверив, одинаковы ли первая и последняя буквы слова и не является ли палиндромом заключенная между ними часть слова (рис. 3.4).

Рис. 3.4.Рекурсивная проверка, является ли слово racecar палиндромом

function palindrome(word)

····if word.length ≤ 1

········return True

····if word.first_char ≠ word.last_char

········return False

····w ← word.remove_first_and_last_chars

····return palindrome(w)

Рекурсивные алгоритмы имеют базовые случаи , когда объем входных данных слишком мал, чтобы его можно было продолжать сокращать. Базовые случаи для функции fib — числа 1 и 2; для функции palindrome это слова, состоящие из единственной буквы или не имеющие ни одной буквы.

Рекурсивные алгоритмы обычно проще и короче итеративных. Сравните эту рекурсивную функцию с power_set из предыдущего раздела, которая не использует рекурсию:

function recursive_power_set(items)

····ps ← copy(items)

····for each e in items

·······ps ← ps.remove(e)

·······ps ← ps + recursive_power_set(ps)

·······ps ← ps.add(e)

····return ps

Эта простота имеет свою цену. Рекурсивные алгоритмы при выполнении порождают многочисленные копии самих себя, создавая дополнительные вычислительные издержки. Компьютер должен отслеживать незаконченные рекурсивные вызовы и их частичные вычисления, что требует большего объема памяти. При этом дополнительные такты центрального процессора расходуются на переключение с одного рекурсивного вызова на следующий и назад.