Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]

Мы уже убедились, что сортировка выбором подчиняется T ( n ) = = n 2+ n — 2. Наиболее быстро растущим членом является n 2, поэтому мы можем записать T ( n ) ≈ n 2. Приняв, что в одной коробке лежит n карточек, мы находим:

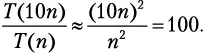
Вам потребуется приблизительно 100 × (2 часа) = 200 часов! А что, если сортировать по другому принципу? Например, есть метод под названием «сортировка пузырьком», временная сложность которого определяется формулой T ( n ) = 0,5 n 2+ 0,5 n . Наиболее быстро растущий член тогда даст T ( n ) ≈ 0,5 n 2, следовательно:

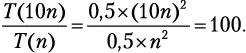
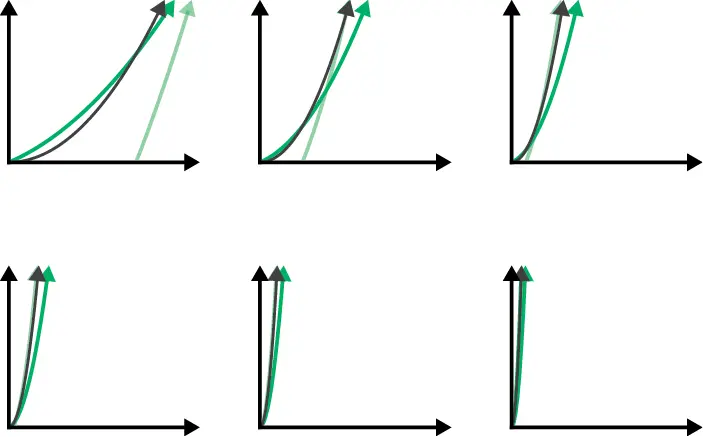
Рис. 2.2.Уменьшение масштаба n 2, n 2+ n — 2 и 0,5 n 2+ 0,5 n с увеличением n

Коэффициент 0,5 сам себя аннулирует! Понять мысль, что оба выражения — n 2— n — 2 и 0,5 n 2+ 0,5 n — растут как n 2, не так-то просто. Почему доминантный член функции игнорирует все другие числа и оказывает наибольшее влияние на рост? Давайте попытаемся эту концепцию представить визуально.

На рис. 2.2 изображены графики двух временных сложностей, которые мы рассмотрели, рядом с графиком n 2на разных уровнях масштабирования. По мере увеличения значения n графики, судя по всему, становятся все ближе и ближе. На самом деле вместо точек в функции T ( n ) = ∙ n 2+ ∙ n + ∙ вы можете подставить любые числа, и она по-прежнему будет расти как n 2.

Запомните, такой эффект сближения кривых работает, если наиболее быстро растущий член — одинаковый. График функции с линейным ростом ( n ) никогда не будет сближаться с графиком квадратичного роста ( n 2), который, в свою очередь, никогда не догонит график, имеющий кубический рост ( n 3).

Вот почему в случаях с очень большими объемами входных данных алгоритмы с квадратично растущей стоимостью показывают худшую производительность, чем алгоритмы с линейной стоимостью, но все же намного лучшую, чем алгоритмы с кубической стоимостью. Если вы все поняли, то следующий раздел будет для вас простым: мы всего лишь познакомимся с необычной формой записи, которую программисты используют для выражения этих идей.

Существует специальная форма записи, которая обозначает классы роста временных затрат: нотация «О большое» . Функция с членом, растущим не быстрее 2 n, обозначается как O (2 n); функция, растущая не быстрее квадратичной, — как O ( n 2); функция с линейным или более пологим ростом — как O ( n ) и т. д. Данная форма записи используется для выражения доминантного члена функций стоимости алгоритмов в худшем случае — это общепринятый способ выражения временной сложности [25] Читаются такие конструкции следующим образом: «алгоритм сортировки имеет временную сложность o-n-квадрат». .

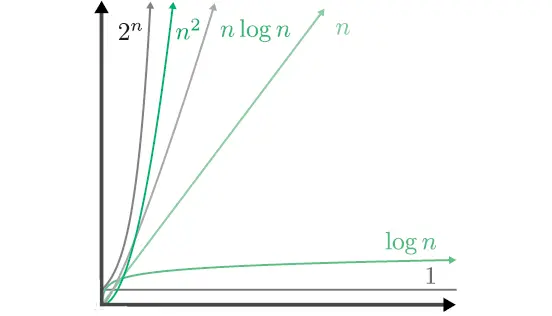
Рис. 2.3.Различные обозначения роста сложности, которые часто можно увидеть внутри O

Сортировка выбором и сортировка пузырьком имеют сложность O ( n 2), но мы вскоре встретим алгоритмы со сложностью O ( n log n ), которые выполняют ту же работу. В случае с O ( n 2) десятикратное увеличение объема входных данных привело к росту стоимости выполнения в 100 раз. Если использовать алгоритм O ( n log n ), то при увеличении объема входных данных в 10 раз стоимость возрастет всего в 10 log 10 ≈ 34 раза.

Когда n равняется миллиону, n 2составит триллион, тогда как n log n — всего лишь несколько миллионов. Работа, на которую алгоритму с квадратично растущей стоимостью потребуются годы, может быть выполнена за минуты алгоритмом со сложностью O ( n log n ). Вот почему при создании систем, обрабатывающих очень большие объемы данных, необходимо делать анализ временной сложности.

При разработке вычислительной системы важно заранее выявить самые частые операции. Затем нужно сравнить «О большое» разных алгоритмов, которые выполняют эти операции [26] По поводу сложностей большого «О» большинства алгоритмов, которые выполняют типовые задачи, смотрите http://code.energy/bigo . . Кроме того, многие алгоритмы работают только с определенными структурами входных данных. Если выбрать алгоритм заранее, можно соответствующим образом структурировать данные.

Есть алгоритмы, которые всегда работают с постоянной продолжительностью, независимо от объема входных данных, — они имеют сложность O (1). Например, проверяя четность/нечетность, мы смотрим, является ли последняя цифра нечетной, — и вуаля! Проблема решена. Скорость решения задачи не зависит от величины числа. С алгоритмами O (1) мы познакомимся подробнее в следующих главах. Они превосходны… впрочем, давайте посмотрим, какие алгоритмы никак нельзя назвать «превосходными».

Мы говорим, что алгоритмы со сложностью O (2 n) имеют экспоненциальное время . Из графика порядков роста (см. рис. 2.3) не похоже, что квадратичные n 2и экспоненциальные сильно отличаются. Если уменьшить масштаб (рис. 2.4), то станет очевидно, что экспоненциальный рост явно доминирует над квадратичным.

Рис. 2.4.Разные порядки роста в уменьшенном масштабе. Линейные и логарифмические кривые растут так медленно, что их уже не видно на графике

Экспоненциальное время растет так быстро, что мы рассматриваем эти алгоритмы как невыполнимые. Они пригодны для очень немногих типов входных данных и требуют значительной вычислительной мощности, если только объем данных не до смешного мал. Не помогут ни оптимизация каждого аспекта программного кода, ни использование суперкомпьютеров. Сокрушительное экспоненциальное время делает эти алгоритмы бесперспективными.

Чтобы наглядно представить взрывной экспоненциальный рост, уменьшим еще масштаб графика и изменим числа (рис. 2.5). Для экспоненциальной функции основание уменьшено с 2 до 1,5 и добавлен делитель 1000. Степенной же показатель увеличен с 2 до 3 и добавлен множитель 1000.

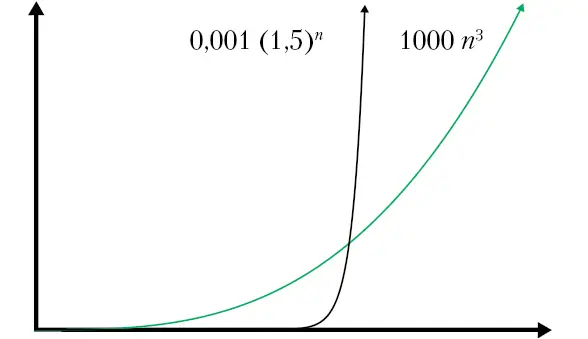
Рис. 2.5.Никакая степенная функция не превзойдет экспоненциальную. На этом графике выбран такой масштаб, что кривой n log n даже не видно из-за ее слишком медленного роста