Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]
- Название:Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]
- Автор:
- Жанр:
- Издательство:Питер
- Год:2018
- Город:СПб.
- ISBN:978-5-4461-0587-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику] краткое содержание
Владстон Феррейра Фило знакомит нас с вычислительным мышлением, позволяющим решать любые сложные задачи. Научиться писать код просто — пара недель на курсах, и вы «программист», но чтобы стать профи, который будет востребован всегда и везде, нужны фундаментальные знания. Здесь вы найдете только самую важную информацию, которая необходима каждому разработчику и программисту каждый день. cite
Владстон Феррейра Фило
Теоретический минимум по Computer Science [Все что нужно программисту и разработчику] - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Шахматные ферзи  У вас есть пустая шахматная доска и 8 ферзей, которые допускается ставить на доске где угодно. Сколькими разными способами можно разместить фигуры?
У вас есть пустая шахматная доска и 8 ферзей, которые допускается ставить на доске где угодно. Сколькими разными способами можно разместить фигуры?
Шахматная доска поделена на 64 клетки, 8 × 8. Число способов выбрать 8 клеток из 64 составляет 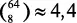 млрд
млрд [19] Профессиональная подсказка: поищите в Интернете по запросу « из 64 по 8 », чтобы узнать результат.
.
Правило суммирования
Подсчет сумм последовательностей часто встречается при решении комбинаторных задач. Суммы последовательных чисел обозначаются прописной буквой «сигма» ( 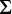 ). Такая форма записи показывает, как выражение будет суммироваться для каждого значения i :
). Такая форма записи показывает, как выражение будет суммироваться для каждого значения i :
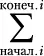 выражение с участием i.
выражение с участием i.
Например, суммирование первых пяти нечетных чисел записывается так:
 .
.
Обратите внимание: чтобы получить слагаемые 1, 3, 5, 7 и 9, вместо i последовательно используются числа от 0 до 4 включительно. Следовательно, сумма первых n натуральных чисел составляет:
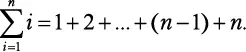
Когда гениальному математику Гауссу было 10 лет, он устал от суммирования натуральных чисел одного за другим по порядку и нашел такой ловкий прием:
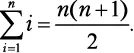
Догадаетесь, каким образом Гаусс это обнаружил? Объяснение приема приведено в приложении II. Давайте посмотрим, как можно его использовать для решения следующей задачи.
Недорогой перелет  Вы должны слетать в Нью-Йорк в любое время в течение следующих 30 дней. Цены на авиабилеты изменяются непредсказуемо в соответствии с датами отъезда и возвращения. Сколько пар дней необходимо проверить, чтобы отыскать самые дешевые билеты для полета в Нью-Йорк и обратно на ближайшие 30 дней?
Вы должны слетать в Нью-Йорк в любое время в течение следующих 30 дней. Цены на авиабилеты изменяются непредсказуемо в соответствии с датами отъезда и возвращения. Сколько пар дней необходимо проверить, чтобы отыскать самые дешевые билеты для полета в Нью-Йорк и обратно на ближайшие 30 дней?
Любая пара дней между сегодняшним (день 1) и последним (день 30) допустима при условии, что возвращение будет в тот же день или позже, чем отъезд. Следовательно, 30 пар начинаются с 1-го дня, 29 пар начинаются со 2-го дня, 28 — с 3-го и т. д. И есть всего одна пара, приходящаяся на последний день. Таким образом, 30 + 29 + … + 2 + 1 — общее количество пар, которое нужно рассмотреть. Мы можем записать это как 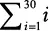 и использовать удобную формулу Гаусса:
и использовать удобную формулу Гаусса:
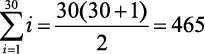 пар.
пар.
Кроме того, мы можем решить эту задачу при помощи комбинаций, выбрав 2 дня из 30. Порядок не имеет значения: на более ранний день придется отъезд, на более поздний — возвращение. Таким образом, мы получим 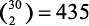 . Что-то не то… Дело в том, что мы должны учесть еще и случаи, когда прибытие и отъезд приходятся на одну дату. Так как дней всего 30, следовательно,
. Что-то не то… Дело в том, что мы должны учесть еще и случаи, когда прибытие и отъезд приходятся на одну дату. Так как дней всего 30, следовательно, 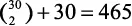 .
.
1.4. Вероятность
Принципы случайности помогут вам разобраться в азартных играх, предсказании погоды или проектировании системы резервного хранения данных с низким риском отказа. Принципы эти просты, и все же большинство людей понимают их неправильно.

Рис. 1.8.Случайное число [20] Любезно предоставлено http://xkcd.com .
Сейчас мы применим наши навыки решения комбинаторных задач к вычислению вероятностей. Затем мы узнаем, каким образом различные типы событий используются для решения задач. Наконец, мы увидим, почему азартные игроки проигрываются в пух и прах.
Подсчет количества возможных вариантов
Бросок кубика имеет шесть возможных результатов: 1, 2, 3, 4, 5 и 6. Шансы получить 4, следовательно, составляют 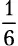 . А какова вероятность выпадения нечетного числа? Это может произойти в трех случаях (когда на кубике будет 1, 3 или 5), потому шансы составляют
. А какова вероятность выпадения нечетного числа? Это может произойти в трех случаях (когда на кубике будет 1, 3 или 5), потому шансы составляют 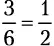 . Вероятность того, что некое событие произойдет, выражается такой формулой:
. Вероятность того, что некое событие произойдет, выражается такой формулой:
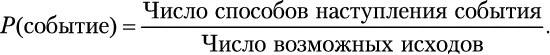
Она работает, потому что каждый возможный исход одинаково вероятен. Кубик имеет ровные грани, и человек, бросающий его, нас не обманывает.
Еще одно формирование команды  Снова 23 человека хотят вступить в вашу команду. В отношении каждого кандидата вы подбрасываете монету и принимаете его, только если она падает «орлом». Какова вероятность, что вы никого не возьмете?
Снова 23 человека хотят вступить в вашу команду. В отношении каждого кандидата вы подбрасываете монету и принимаете его, только если она падает «орлом». Какова вероятность, что вы никого не возьмете?
Мы уже убедились, что существует 2 23= 8 388 608 возможных вариантов состава команды. Вам придется рассчитывать только на себя в одном-единственном случае: если в результате подбрасывания монеты выпадут 23 «решки» подряд. Вероятность такого события равна P (никто) =  . Если посмотреть на это с высоты птичьего полета, то вероятность того, что конкретный рейс коммерческой авиакомпании потерпит крушение, составляет порядка 1 из 5 млн.
. Если посмотреть на это с высоты птичьего полета, то вероятность того, что конкретный рейс коммерческой авиакомпании потерпит крушение, составляет порядка 1 из 5 млн.
Независимые (совместные) события
Если вы одновременно бросаете монету и кубик, то шанс получить «орел» и 6 равняются 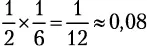 , или 8 %. Когда исход одного события не влияет на исход другого, их называют независимыми . Вероятность получить сочетание конкретных результатов двух независимых событий равна произведению вероятностей каждого из них.
, или 8 %. Когда исход одного события не влияет на исход другого, их называют независимыми . Вероятность получить сочетание конкретных результатов двух независимых событий равна произведению вероятностей каждого из них.
Резервное хранение  Вам нужно организовать хранение данных в течение года. Один диск имеет вероятность сбоя 1 на 1 млрд. Другой стоит 20 % от цены первого, но в его случае вероятность сбоя — 1 на 2000. Какой диск вам следует купить?
Вам нужно организовать хранение данных в течение года. Один диск имеет вероятность сбоя 1 на 1 млрд. Другой стоит 20 % от цены первого, но в его случае вероятность сбоя — 1 на 2000. Какой диск вам следует купить?
Интервал:
Закладка:
![Обложка книги Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]](/books/1060455/vladston-ferrejra-filo-teoreticheskij-minimum-po-co.webp)









