Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]

Формирование команды Допустим, 23 человека хотят вступить в вашу команду. В отношении каждого кандидата вы подбрасываете монету и принимаете его, только если выпадет «орел». Сколько всего может быть вариантов состава команды?

До начала набора есть всего один вариант состава — вы сами. Далее каждый бросок монеты удваивает число возможных вариантов. Это должно быть сделано 23 раза, таким образом, вам нужно посчитать, чему равно 2 в степени:

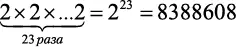вариантов команды.

Обратите внимание, что один из этого множества вариантов — когда в команде состоите только вы.

Если у нас n элементов, то мы можем упорядочить их n ! разными способами. Факториал числа имеет взрывной характер, даже с малыми значениями n он дает огромные числа. На случай, если вы с ним не знакомы:

n ! = n × ( n — 1) × ( n — 2) … × 2 × 1.

Легко заметить, что n ! — это общее количество способов упорядочивания n элементов. Сколькими способами можно выбрать первый элемент из n ? После того как он будет выбран, сколькими способами можно выбрать второй? Сколько вариантов останется для третьего? Подумайте об этом некоторое время, а потом переходите к примерам [17] По определению 0! = 1. Мы говорим, что ноль элементов, то есть пустое множество, можно упорядочить единственным способом. .

Коммивояжер Ваша транспортная компания осуществляет поставки в 15 городов. Вы хотите знать, в каком порядке лучше объезжать эти города, чтобы уменьшить расход топлива. Если на вычисление длины одного маршрута требуется микросекунда, то сколько времени займет вычисление длины всех возможных маршрутов?

Любая перестановка 15 городов дает новый маршрут. Факториал — это количество различных комбинаций, так что всего существует 15! = 15 × 14 × … × 1 ≈ 1,3 трлн маршрутов. Число микросекунд, которые уйдут на их вычисление, примерно эквивалентно 15 дням. Будь у вас не 15, а 20 городов, вам бы понадобилось 77 тысяч лет.

Совершенная мелодия Девушка разучивает гамму из 13 нот. Она хочет, чтобы вы показали все возможные мелодии, в которых используется 6 нот. Каждая нота должна встречаться один раз на мелодию, а каждая такая мелодия должна звучать в течение одной секунды. О какой продолжительности звучания идет речь?

Мы должны подсчитать количество комбинаций по 6 нот из 13. Чтобы исключить неиспользуемые ноты, нужно остановить вычисление факториала после шестого множителя. Формально 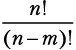— это количество возможных комбинаций m из n возможных элементов. В нашем случае получится:

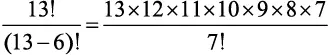
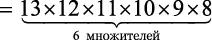
= 1 235 520 мелодий.

Чтобы их все прослушать, потребуется 343 часа, так что вам лучше убедить девушку найти идеальную мелодию каким-нибудь другим путем.

Факториал n ! дает завышенное число способов упорядочивания n элементов, если некоторые из них одинаковые. Лишние комбинации, где такие элементы просто оказываются на других позициях, не должны учитываться.

Если в последовательности из n элементов r идентичны, существуют r ! способов переупорядочить их. То есть n ! включает r ! таких комбинаций. Чтобы получить число уникальных комбинаций, нужно разделить n ! на этот излишек. Например, число различных сочетаний букв E в CODE ENERGY равняется .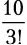

Игры с ДНК Биолог изучает сегмент ДНК, связанный с генетическим заболеванием. Тот состоит из 23 пар нуклеотидов, где 9 должны быть A — T, а 14 — G — C.

Ученый хочет выполнить моделирование на всех возможных сегментах ДНК, где есть такое количество пар нуклеотидов. Сколько задач ему предстоит выполнить?

Сначала вычислим все возможные комбинации этих 23 пар нуклеотидов. Затем, чтобы учесть повторяющиеся пары нуклеотидов A-T и G-C, разделим результат на 9! и на 14! и получим:

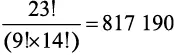вариантов.

Но задача еще не решена. Нужно учесть ориентацию пар нуклеотидов.

Следующие два примера не тождественны:

Для каждой последовательности из 23 пар нуклеотидов существует 2 23различных сочетаний ориентации. Потому общее количество комбинаций равно:

817 190 × 2 23≈ 7 трлн.

И это только для крошечной последовательности всего из 23 пар нуклеотидов, где мы знаем распределение! Наименьшая воспроизводимая ДНК, которая известна на сегодняшний день, — это ДНК крохотного цирковируса свиней, и в ней 1800 пар нуклеотидов. Код ДНК и жизнь в целом с технологической точки зрения по-настоящему удивительны. Просто с ума можно сойти: ДНК человека имеет около 3 млрд пар нуклеотидов, продублированных в каждой из 3 трлн клеток тела.

Представьте колоду из 13 игральных карт только пиковой масти . Сколькими способами вы сможете раздать шесть карт своему сопернику? Мы уже видели, что 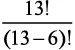— это количество перестановок 6 карт из 13. Поскольку порядок их следования не имеет значения, нужно разделить это число на 6! чтобы получить

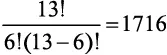комбинаций.

Бином 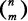— это количество способов, которыми можно извлечь m элементов из ряда, состоящего из n элементов, независимо от порядка их следования:

Конструкция в левой части (запись бинома) читается как «из n по m » [18] В литературе принято обозначение ( m — нижний индекс, n — верхний), которое читается как «сочетания m из n ». — Примеч. пер. .