Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]

Двусторонняя условная зависимость.Обратите внимание, что высказывание « Если вода в бассейне теплая, то я буду плавать » не означает: «Я буду плавать только в теплой воде». Данное высказывание ничего не говорит насчет холодных бассейнов. Другими словами, A 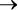B не означает B 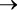A . Чтобы выразить оба условных суждения, используйте двустороннюю условную зависимость :

A <���—> B : Я буду плавать, если и только если вода в бассейне теплая.

Здесь теплая вода в бассейне равнозначна тому, что я буду плавать: знание о воде в бассейне означает знание о том, что я буду плавать, и наоборот. Опять же, остерегайтесь обратной ошибки : никогда не предполагайте, что B 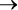A следует из A 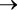B .

AND, OR и XOR.Эти логические операторы — самые известные, поскольку они часто записываются в исходном коде в явном виде — AND (И), OR (ИЛИ) и XOR (исключающее ИЛИ). AND возвращает True, если все идеи истинны; OR возвращает True, если любая идея истинна; XOR возвращает True, если идеи взаимоисключающие. Представим вечеринку, где подают водку и вино:

A : Вы пили вино.

B : Вы пили водку.

A OR B : Вы пили.

A AND B : Вы пили и то и другое.

A XOR B : Вы пили, не смешивая.

Проверьте, правильно ли вы понимаете, как работают эти операторы. В табл. 1.1 перечислены все возможные комбинации двух переменных. Обратите внимание, что A B тождественно! A OR B , а A XOR B тождественно!( A <���—> B ).

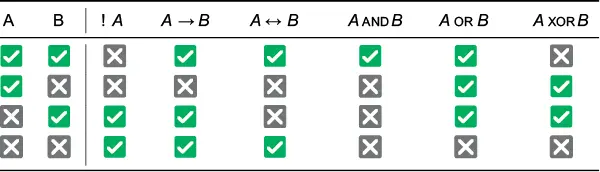
Таблица 1.1.Логические операции для четырех возможных комбинаций A и B

Булева алгебра [10] Названа так в честь Джорджа Буля (1815–1864). Его публикации положили начало математической логике. позволяет упрощать логические выражения точно так же, как элементарная алгебра упрощает числовые.

Ассоциативность.Для последовательностей, состоящих только из операций AND или OR, круглые скобки не имеют значения. Так же, как последовательности только из операций сложения или умножения в элементарной алгебре, эти операции могут вычисляться в любом порядке.

A AND ( B AND C ) = ( A AND B ) AND C ;

A OR ( B OR C ) = ( A OR B ) OR C .

Дистрибутивность.В элементарной алгебре мы раскрываем скобки: a × (b + c) = (a × b) + (a × c). Точно так же и в логике выполнение операции AND после OR эквивалентно выполнению операции OR над результатами операций AND и наоборот:

A AND ( B OR C ) = ( A AND B ) OR ( A AND C );

A OR ( B AND C ) = ( A OR B ) AND ( A OR C ).

Правило де Моргана [11] Огастес де Морган дружил с Джорджем Булем. Кроме того, он обучал молодую Аду Лавлейс, ставшую первым программистом за век до того, как был создан первый компьютер. . Одновременно лета и зимы не бывает, поэтому у нас либо не лето, либо не зима. С другой стороны, оба выражения «не лето» и «не зима» истинны , если (и только) у нас не тот случай, когда либо лето, либо зима. Согласно этой логике, выполнение операций AND может быть сведено к операциям OR и наоборот:

!( A AND B ) =! A OR! B ;

! A AND! B =!( A OR B ).

Эти правила позволяют преобразовывать логические модели, раскрывать их свойства и упрощать выражения. Давайте решим задачу.

Перегрев сервера Сервер выходит из строя из-за перегрева, когда кондиционирование воздуха выключено. Он также выходит из строя из-за перегрева, если барахлит кулер. При каких условиях сервер работает?

Моделируя эту задачу в логических переменных, можно в одном выражении сформулировать условия, когда сервер выходит из строя:

A: Сервер перегревается.

B : Кондиционирование отключено.

C: Не работает кулер.

D: Сервер вышел из строя.

( A AND B ) OR ( A AND C ) 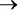D .

Используя правило дистрибутивности, выведем за скобки A :

A AND ( B OR C ) 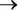D .

Сервер работает, когда! D . Противопоставление записывается так:

! D 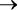!( A AND ( B OR C )).

Применим правило де Моргана и раскроем скобки:

! D 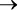! A OR!( B OR C ).

Воспользуемся правилом де Моргана еще раз:

! D 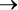! A OR (! B AND! C ).

Данное выражение нам говорит, что когда сервер работает, мы имеем либо! A (он не перегревается), либо! B AND! C (все в порядке и с кондиционированием воздуха, и с кулером).

Еще один способ анализа логических моделей состоит в сверке данных со всевозможными сочетаниями ее переменных. Каждой переменной в таблице истинности соответствует свой столбец. Строки представляют комбинации состояний переменных.

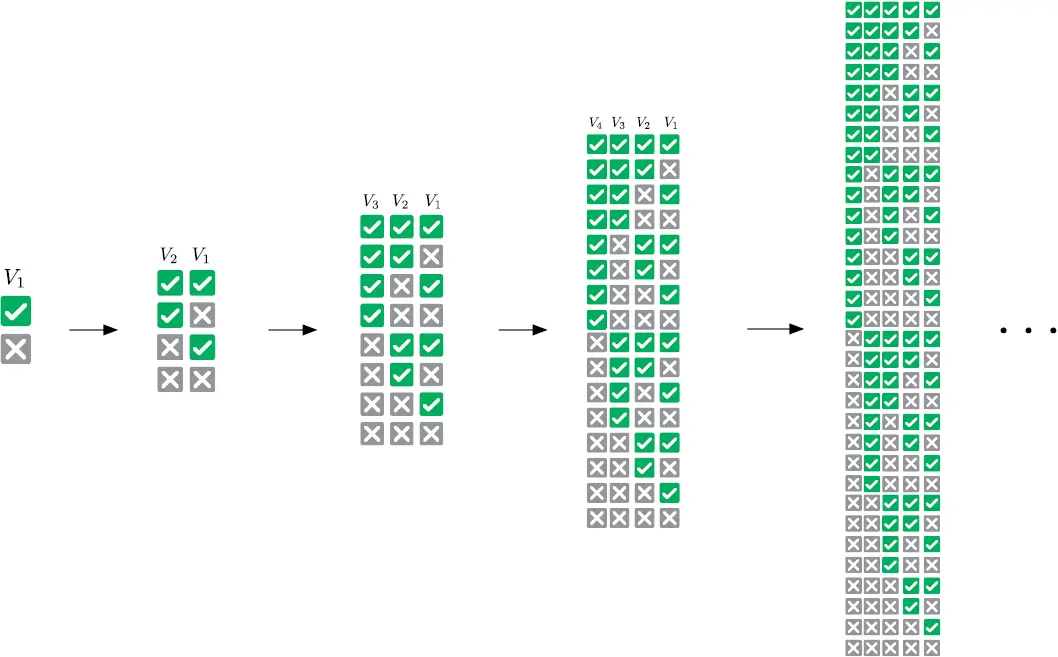
Рис. 1.5.Таблицы со всеми возможными сочетаниями от одной до пяти логических переменных

Одна переменная требует двух строк: в одной она имеет значение True, в другой — False. Чтобы добавить переменную, нужно удвоить число строк. Новой переменной задается True в исходных строках и False — в добавленных (рис. 1.5). Размер таблицы истинности увеличивается вдвое с каждым добавлением переменной, поэтому такую таблицу оправданно использовать лишь в случаях, когда переменных немного [12] Например, таблица истинности для 30 переменных будет иметь более миллиарда строк . .

Давайте посмотрим, как можно использовать таблицу истинности для анализа задачи.

Хрупкая система Предположим, что мы должны создать систему управления базами данных с соблюдением следующих технических требований: