Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]

Эту проблему можно наглядно увидеть на деревьях рекурсивных вызовов — диаграммах, показывающих, каким образом алгоритм порождает новые вызовы, углубляясь в вычисления. Мы уже видели деревья рекурсивных вызовов для поиска чисел Фибоначчи (см. рис. 3.3) и для проверки слов-перевертышей (см. рис. 3.4).

Если требуется максимальная производительность, то можно избежать этих дополнительных издержек, переписав рекурсивный алгоритм в чисто итеративной форме. Такая возможность есть всегда. Это компромисс: итеративный программный код обычно выполняется быстрее, но вместе с тем он более громоздкий и его труднее понять.

Полный перебор, он же метод «грубой силы», предполагает перебор всех случаев, которые могут быть решением задачи. Эта стратегия также называется исчерпывающим поиском. Она обычно прямолинейна и незамысловата: даже в том случае, когда вариантов миллиарды, она все равно опирается исключительно на силу , то есть на способность компьютера проверить их все.

Рис. 3.5.Простое объяснение: полный перебор [31] Любезно предоставлено http://geek-and-poke.com .

Давайте посмотрим, как ее можно использовать, чтобы решить следующую задачу.

Лучшая сделка У вас есть список цен на золото по дням за какой-то интервал времени. В этом интервале вы хотите найти такие два дня, чтобы, купив золото, а затем продав его, вы получили бы максимально возможную прибыль.

Не всегда у вас получится сделать покупку по самой низкой цене, а продать по самой высокой: первая может случиться позже второй, а перемещаться во времени вы не умеете. Алгоритм полного перебора позволяет просмотреть все пары дней . По каждой паре он находит прибыль и сравнивает ее с наибольшей, найденной к этому моменту. Мы знаем, что число пар дней в интервале растет квадратично по мере его увеличения [32] В интервале n дней имеется n (n + 1)/2 пар дней (см. раздел «Комбинаторика» главы 1). . Еще не приступив к написанию кода, мы уже уверены, что он будет иметь O ( n 2).

Задача о лучшей сделке решается и с помощью других стратегий с меньшей временной сложностью — мы вскоре их рассмотрим. Но в некоторых случаях наилучшую временную сложность дает подход на основе полного перебора. Это имеет место в следующей задаче.

Рюкзак У вас есть рюкзак, вы носите в нем предметы, которыми торгуете. Его вместимость ограничена определенным весом, так что вы не можете сложить в него весь свой товар. Вы должны выбрать, что взять. Цена и вес каждого предмета известны, вам нужно посчитать, какое их сочетание дает самый высокий доход.

Степенное множество ваших предметов [33] Подробнее о степенных множествах см. в приложении III. содержит все возможные их сочетания. Алгоритм полного перебора просто проверяет эти варианты. Поскольку вы уже знаете, как вычислять степенные множества, алгоритм не должен вызвать у вас затруднений:

function knapsack(items, max_weight)

····best_value ← 0

····for each candidate in power_set(items)

········if total_weight(candidate) ≤ max_weight

············if sales_value(candidate) > best_value

················best_value ← sales_value(candidate)

················best_candidate ← candidate

····return best_candidate

Для n предметов существует 2 n подборок. В случае каждой из них мы проверяем, не превышает ли ее общий вес вместимости рюкзака и не оказывается ли общая стоимость подборки выше, чем у лучшей, найденной к этому времени. Иными словами, для каждой подборки выполняется постоянное число операций, а значит, алгоритм имеет сложность O (2 n).

Однако проверять следует не каждую подборку предметов. Многие из них оставляют рюкзак полупустым, а это указывает на то, что существуют более удачные варианты [34] Задача о рюкзаке является частью класса NP-полных задач, который мы обсудили в разделе 2.3. Вне зависимости от стратегии ее решают только экспоненциальные алгоритмы. . Далее мы узнаем стратегии, которые помогут оптимизировать поиск решения, эффективным образом отбраковывая неподходящие варианты.

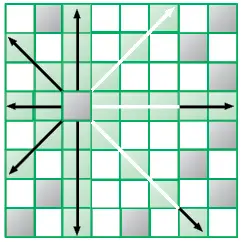
Вы играете в шахматы? Фигуры перемещаются на доске 8 × 8 клеток и поражают фигуры соперника. Ферзь — это самая сильная фигура: она поражает клетки по горизонтали, по вертикали и по двум диагоналям. Следующая стратегия будет объяснена в контексте известной шахматной задачи.

Задача о восьми ферзях Как разместить восемь ферзей на доске так, чтобы ни один из них не оказался под ударом других?

Попробуйте найти решение вручную, и вы увидите, что оно далеко не тривиальное. Рис. 3.6 показывает один из способов расположения мирно сосуществующих ферзей.

В разделе 1.3 мы видели, что восемь ферзей можно разместить на шахматной доске более чем 4 млрд способами. Решение искать ответ полным перебором, проверяя все варианты, я бы назвал неосмотрительным. Предположим, что первые два ферзя помещены на доску таким образом, что представляют угрозу друг для друга. Тогда независимо от того, где окажутся следующие ферзи, решение найти не удастся. Подход на основе полного перебора не учитывает этого и будет впустую тратить время, пытаясь разместить всех обреченных ферзей.

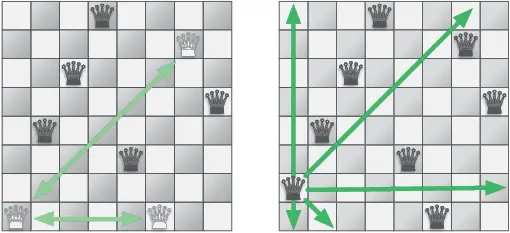
Рис. 3.6.Крайний левый ферзь может бить двух других. Если переместить его на одну клетку вверх, то он не будет никому угрожать

Более эффективный поход состоит в поиске только приемлемых позиций для фигур. Первого ферзя можно поместить куда угодно. Приемлемые позиции для каждого следующего будут ограничены уже размещенными фигурами: нельзя ставить ферзя на клетку, находящуюся под ударом другого ферзя. Если мы начнем руководствоваться этим правилом, мы, вероятно, получим доску, где невозможно разместить дополнительного ферзя, еще до того, как число фигур дойдет до восьми (рис. 3.7).

Это будет означать, что последнего ферзя мы разместили неправильно. Потому нам придется отойти назад — вернуться к предыдущей позиции и продолжить поиск. В этом заключается суть стратегии поиска с возвратом: продолжать размещать ферзей в допустимые позиции. Как только мы окажемся в тупике, мы отойдем назад, к моменту, предшествовавшему размещению последнего ферзя. Этот процесс можно оптимизировать при помощи рекурсии: