Денис Соломатин - Основы статистической обработки педагогической информации

2. Существует положительная корреляция между результативностью и элементарно предоставляемой возможностью бить по мячу. Дело в том, что команды контролируют свой состав, поэтому очевидно, что на поле выходят только лучшие игроки из лучших.

Предварительно преобразуем сведения об ударах игроков в табличную форму, так они легче воспринимаются:

удары <���– as_tibble(Lahman::Batting)

эффективность <���– удары %>%

group_by(playerID) %>%

summarise(

результативность = sum(H, na.rm = TRUE) / sum(AB, na.rm = TRUE),

возможность = sum(AB, na.rm = TRUE)

)

эффективность %>%

filter(возможность > 100) %>%

ggplot(mapping = aes(x = возможность, y = результативность)) +

geom_point() +

geom_smooth(se = FALSE)

Функция geom_smooth() здесь формирует график методом обобщенных аддитивных моделей с интегрированной оценкой гладкости (method = "gam") рассчитывая значения по формуле formula = y ~ s(x, bs = "cs"), так как имеется более 1 000 наблюдений.

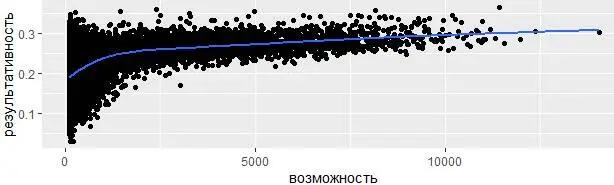
Особый интерес вызывает ранжирование результатов. Если наивно отсортировать показатели эффективности по убыванию результативности, то первыми с самой лучшей результативностью окажутся скорее везучие, а не квалифицированные игроки, за всю карьеру сделавшие лишь 1 удар, но при этом попавшие по мячу:

эффективность %>%

arrange(desc(результативность))

Можно найти хорошее объяснение этого парадокса в пословице «новичкам везёт». Используя простые инструменты, подсчет количества одинаковых значений, их суммирование, можно долго искать любопытные закономерности, но R предоставляет и много других полезных функций для генерации статистических отчетов:

Выше использовалась функция, вычисляющая среднее значение mean( x ), но вычисляющая медианное значение функция median( x ) тоже бывает полезна. Ведь среднее как 36.6° по больнице, а медиана – это величина, относительно которой 50% значений x находится выше, и 50% находится ниже, что гораздо информативнее. Иногда полезно комбинировать подобные функции с логическим условием. Мы еще не говорили о таких вещах как подмножество значений, этому можно посвятить целый раздел, пока лишь приведем наглядный пример, на тех же неотмененных авиарейсах, сгруппированных по дате вылета.

Отрицательные значения «задержки» рейса символизируют прибытие с опережением графика, оказывается, такое тоже бывает:

неотмененные %>% group_by(year, month, day) %>%

summarise(

средняя_задержка = mean(arr_delay),

средняя_положительная_задержка = mean(arr_delay[arr_delay > 0])

)

Особый интерес вызывают функции вычисления стандартного отклонения sd(x), меры разброса наблюдаемой величины, вычисления интерквартильного размаха IQR(x) и вычисления медианы абсолютного отклонения mad(x), которые являются надежными эквивалентами друг друга и могут быть полезны, если у данных есть выбросы. Любопытно, почему расстояние до одних пунктов назначения варьируются сильнее, чем до других, являя собой не иначе как чудеса телепортации:

неотмененные %>% group_by(dest) %>%

summarise(среднеквадратическое_отклонение_дистанции = sd(distance)) %>%

arrange(desc(среднеквадратическое_отклонение_дистанции))

Функции поиска минимального значение min(x), первого квантиля quantile(x, 0.25), вычисления максимума max(x), неизменные спутники при построении ранжирования. Квантили являются обобщением медианы. Так, например, quantile(x, 0.25) найдет значение x , которое больше чем 25% значений из всех возможных значений анализируемой переменной, и меньше чем остальные 75%.

Найдем время отправления первого и последнего рейса каждый день:

неотмененные %>% group_by (year, month, day) %>%

summarise( первый_рейс = min (dep_time),

последний_рейс = max (dep_time) )

Измерение позиции указателя на элементах списка осуществляется функциями first( x ) для выбора первого элемента переменной x , nth( x , n ) для выбора n -ного, last( x ) для выбора последнего. Они работают аналогично адресации массивов в нотации x [1], x [ n ] и x [length( x )], но возвращают значение аргумента default, если запрошенная позиция не существует. Например, не увенчается успехом попытка получить значение такого элемента, как неотмененные$dep_time[length(неотмененные$dep_time)+1], вернув NA, неопределенное значение переменной, но при этом на выходе даст «Бинго!» вызов nth(неотмененные$dep_time,length(неотмененные$dep_time)+1, default = "Бинго!").

Следующая функция range() дополняет фильтрацию. Приведём пример, в котором сначала все записи группируются по датам и ранжируются, а потом фильтрация оставляет в строках значения, имеющие наибольший и наименьший из рангов в группе. Для сравнения, вызов функции range(неотмененные$dep_time) вернёт список, состоящий из наибольшего и наименьшего значений переменной dep_time:

неотмененные %>% group_by (year, month, day) %>%

mutate(ранжирование = min_rank(desc(dep_time))) %>%

filter(ранжирование %in% range(ранжирование) )

Ранее в вычислениях уже использовалась функция n(), которая вызывается без аргументов, и возвращает размер текущей группы. Чтобы посчитать количество непустых значений в группе х , используется конструкция sum(!is.na( x )), а чтобы подсчитать число различных (уникальных) значений вызывается n_distinct( x ). Например, вычислим, какие направления имеют наибольшее количество перевозчиков:

неотмененные %>% group_by(dest) %>%

summarise(перевозчики= n_distinct(carrier)) %>%

arrange(desc(перевозчики))

Подсчеты значений настолько востребованы, что в пакете dplyr выделена отдельная функция count() для этого. Подсчитаем число повторений каждого направления, хранящихся в переменной dest таблицы неотмененных авиарейсов:

неотмененные %>% count(dest)

При необходимости указывается параметр веса каждого слагаемого (wt). Например, это можно использовать для подсчета общей суммы количества миль, которые пролетел самолет с фиксированным бортовым номером, взятым из поля talinum в базе неотмененных рейсов:

неотмененные %>% count(tailnum, wt = distance)

Подсчет числа значений удовлетворяющих логическому выражению, sum( x > 777), или их среднее количество, mean( y == 0), предполагает, что в связке с числовыми функциями TRUE преобразуется в 1, а FALSE в 0. Это делает функции sum() и mean() очень востребованными: sum( x ) возвращает количество значений TRUE для аргумента x , а mean( x ) возвращает их долю. Вычислим, сколько неотмененных рейсов было до 6 утра по данным за каждые сутки, это обычно указывает на задержку с предыдущего дня:

неотмененные %>% group_by(year, month, day) %>%

summarise(утренние_рейсы = sum(dep_time < 600))

Какова доля неотмененных рейсов, задержавшихся более часа:

неотмененные %>% group_by(year, month, day) %>%

summarise(часовая_задержка = mean(arr_delay >= 61))

При группировании по нескольким переменным, каждая новая сводка выносится на новый уровень группировки. Это облегчает восприятие и постепенно упрощает данные: