Жак Арсак - Программирование игр и головоломок

Отсюда получаем схему операции сложения:

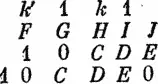
Запишем, что A + B + C + D + E + F + G + H + I + J = 45,

А = 1, B = 0.

Запишем пять операций сложения с учетом переносов в старший разряд:

J + E = 10,

1 + I + D = 10 k + E ,

k + H + C = 10 + D ,

1 + G + В = 10 k ' + С ,

k ' + F + A = 10.

Сложим их все. Вам остается

C + D + E = 17 − 9( k + k ').

Но С + D + E не может быть меньше, чем 2 + 3 + 4 = 9, и не может быть больше, чем 6 + 7 + 9 (если F = 8 и k ' = 1). Не может быть, чтобы у вас одновременно выполнялись соотношения k = k ' = 1 (что давало бы отрицательную сумму С + D + E ). Но не может быть и равенства k + k ' = 1, так как тогда было бы С + D + E = 17 − 9 = 8, что слишком мало. Следовательно, k = k ' = 0. Составим окончательную систему

J + E = 10,

I + D + 1 = E ,

H + C = 10 + D ,

G + 1 = С ,

F = 9.

Закончите вы с помощью программы.

Головоломка 11.

Обозначим через a i цифры исходного числа, b i — цифры результата, k i — цифры «в уме»:

3 a i + k i = b i + 10 k i +1.

Сумма всех a i равна 45, как и сумма всех b i . Обозначим через K сумму всех k i :

3*45 + K = 45 + 10* K дает К = 10.

Мы знаем, что дает «в уме» каждая цифра:

1 дает 0, 2 дает 0, 3 дает 0 или 1 в зависимости от того, что хранится «в уме» над 3.

4 дает 1, 5 дает 1, 6 дает 1, потому что не может случиться 3*6 + 2, что давало бы «в уме» 2, но цифру единиц 0;

7, 8 и 9 дают 2.

Для того, чтобы сумма величин «в уме» была равна 10, нужно, чтобы 3 давало 1 «в уме». Так как 3*3 + 1 (с цифрой единиц, равной 0) случиться не может, то нужно, чтобы «в уме» над 3 было 2. Следовательно, 3 стоит слева от 7, 8 или 9. В частности, 3 не может стоять на правом конце.

Остальное просто, если вы будете следовать методу, указанному в разделе «Условия». Вот таблица:

Потребуем, чтобы 9 было справа; следовательно, вычеркнем 9 из этой таблицы, оставив его только в столбце, соответствующей тому, что «в уме» 0. Цифра 3 требует 2 «в уме», чтобы дать 1. Вычеркнем остальные 3 в таблице. Цифра 9 не может быть получена иначе как с помощью 6 и 1 «в уме». Другие 6 вычеркиваем. Цифра 8 получается из 2 при 2 «в уме». Нужно взять 3 числа в первом столбце, так что нужно еще одно не равное ни 2, ни 3. Их нужно 4 в среднем столбце, так что нужно еще 3 числа, ре равных 6, которые нужно взять среди цифр 7, 4, 1, 8, 5. Два последних числа должны быть взяты из столбца с нулем «в уме». Когда эти числа среди всех возможных будут выбраны, останется расположить их в соответствии с тем, что должно быть для них «в уме». Эту программу сделать легко.

Головоломка 12.

Если число a 1 a 2… a p (представленное как последовательность цифр) кратно 3, то и a 1+ а 2+ … + a p кратно 3. Сумма кубов цифр равна

a 1 3+ а 2 3+ … + a p 3.

Нужно показать, что это число также кратно 3. Действуйте по индукции по числу слагаемых. Предположим, что для p = n − 1 членов

a 1 3+ а 2 3+ … + a p 3= ( a 1+ … + a p ) 3по модулю 3; тогда равенство

( a 1+ … + a p + a n ) 3= ( a 1+ … + a p ) 3+ a n 3+ 3 (…)

доказывает наше утверждение для n слагаемых.

Возьмите число с k цифрами. Сумма кубов его цифр ограничена величиной k *9 3. Но исходное число не может быть меньше, чем 10 k−1. Следовательно, достаточно, чтобы 10 k−1было больше, чем k *729, что очевидным образом выполняется при k = 5. Но эта оценка слишком пессимистична.

Головоломка 14.

Число, полученное при обращении порядка цифр, равно

1000 d + 100 c + 10 b + a ,

и разность этих двух чисел равна

999 ( a − d ) + 90 ( b − c ).

Числа a , b , c , d были расположены в невозрастающем порядке, и они не все равны между собой, так что a строго больше d и a − d не равно нулю. Все остальное просто.

Головоломка 16.

Единственное, что до сих пор еще не сказано — это способ определять, становится» ли последовательность периодической. Метод Полларда был основан на первой стратегии. Мы выясняем, существует ли a i с a 2 i = a i . Но вычисление f ( x ) = x 2− 1 по модулю n — дорогое вычисление. Брепт улучшил этот метод, предложив использовать вторую стратегию.

Головоломка 17.

Эта программа основана на следующих результатах:

если b нечетно, n четно, то n делится на b тогда и только тогда, когда n /2 делится на b ;

нечетное n делится на b тогда и только тогда, когда n − b делится на b . Но n − b четно.

Для n = 2 77− 3 и b = 7 вы получаете:

Число n нечетно. Рассматриваем n − b = 2 77− 10. Оно делится на 2: получаем 2 76− 5.

Это число нечетно: (2 76− 5) − 7 = 2 76− 12.

Делим на 4: 2 74— 3.

Получаем ту же самую задачу, в которой показатель уменьшен на 3. Так как 77 = 3*25 + 2, то мы таким образом доходим до 2 2— 3 = 1, которое не делится на 3. Вряд ли вас слишком утомит доказательство того, что 2 n − 3 никогда не делится на 7…

Головоломка 18.

Я не в состоянии рассказать вам, как я получил эту программу, это — очень долгая история, связанная с разложением целых чисел на множители. Может быть, когда-нибудь я ее и опубликую. Следовательно, будем разбираться в том, что нам дано — в тексте программы.

Начнем с нечетного n . В соответствии с инициализацией программы n = 4 p − 1, где p четно. В противном случае уже последует ответ «НЕТ». Следовательно, рассмотрите нечетное n , являющееся полным квадратом и, следовательно, квадратом нечетного числа 2 k + 1;

(2 k + 1) 2= 4 k 2+ 4 k + 1 = 4 k ( k + 1) + 1.

Так как k ( k + 1) — произведение двух последовательных целых чисел, и из двух последовательных целых чисел всегда есть хотя бы одно четное число, получаем простой, но интересный результат: любой квадрат нечетного числа сравним с 1 по модулю 8. Таким-образом, при n отличном от 1 по модулю 8 инициализирующая часть программы выводит, что n не является точным квадратом.

Посмотрим теперь, что происходит внутри цикла. Делим p на 2, и если результат четен, мы удовлетворяемся тем, что умножаем a на 2. При этом действии произведение a * p остается постоянным. Поэтому кажется вероятным, что в цикле существует инвариантная величина, запись которой содержит a * p в предположении, что p четно.